Question

Построить график функции:
y=-x^2+6x-5
Найдите за графиком:
а)точки пересечения графика с осями координат
б)нули функции промежутки в которых y<0, y>0
в)промежуток возрастаниям и падения функции
г)наибольшее и наименьшее значение функции

Answer 1

$-x^2 + 6x-5$

$x_0 = -frac b{2a} = 3\y_0 = -9 + 18 -5 = 4$

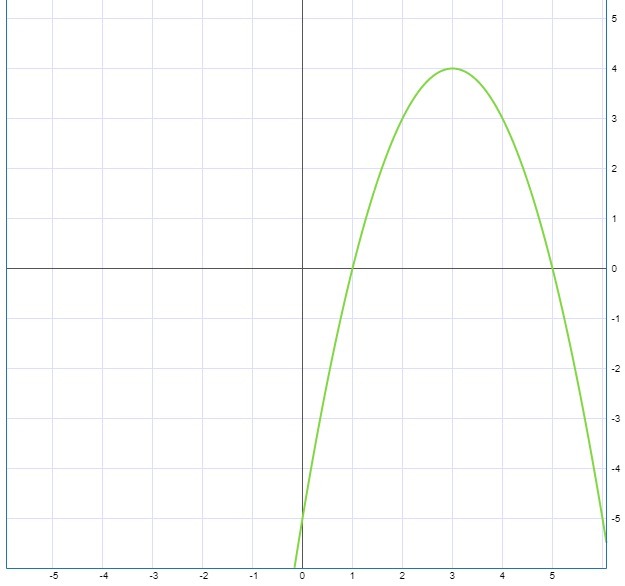
График будет таков:

https://ru-static.z-dn.net/files/d7b/97e7843dea9d1bb640e375ce2f38cbd8.png

1) Точки пересечения с OX: x = 1; x= 5.

Точки пересечения с OY: y = -5;

2) y > 0 (1; 5); y < 0 (-∞; 1) ∪ (5; ∞)

3) y ↑ (-∞; 3); y ↓ (3; ∞)

4) Наибольшее значение: y = 4; Наименьшего значения не имеется

Answer 2

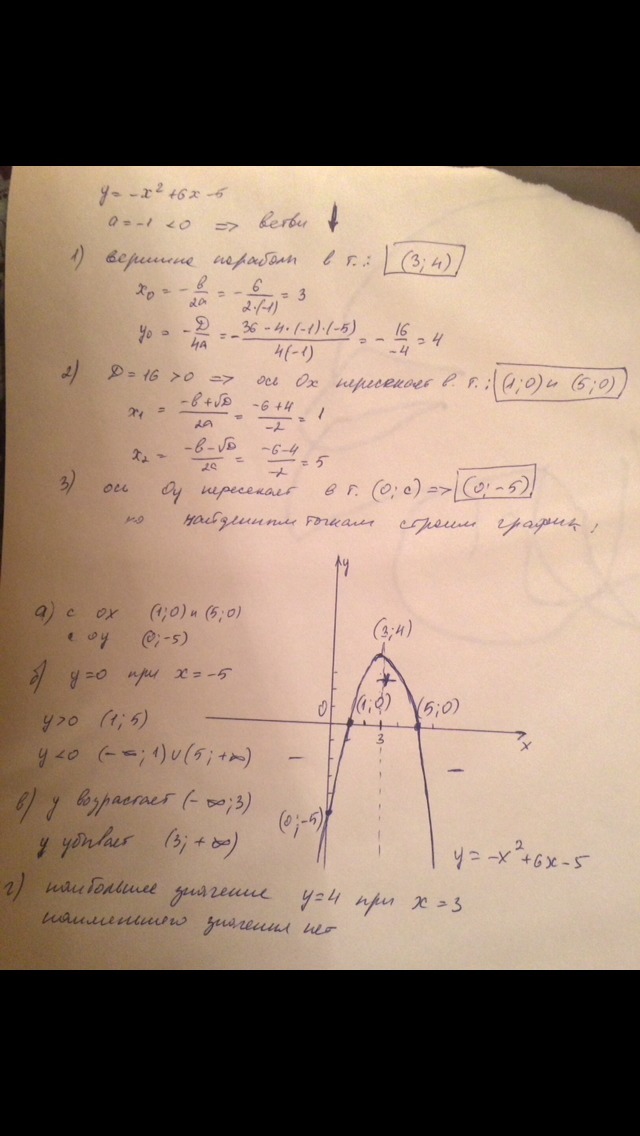
График представляет собой параболу у=х^2, сдвинутый по оси Ох вправо на 3 ед, по оси Оу вверх на 4 единицы.