Задание во вложении. (В основании пирамиды SABCD лежит прямоугольник ABCD со стороной AB=3 и диагональю BD=5...)
Приложения:

Ответы
Ответ дал:
0
..............................................
Приложения:
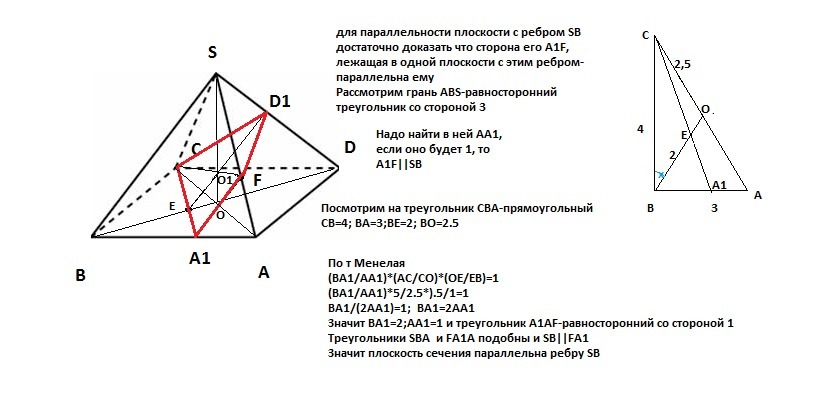
Ответ дал:
0
Перехвалил я тебя Олежа. Признак параллельности прямой и плоскости не знаешь )))
Ответ дал:
0
Я такой тупой
Ответ дал:
0
А у Вас там во второй строчке т. Менелая какая-то опечатка...
Ответ дал:
0
Как вы OE нашли?
Ответ дал:
0
А, понял, у Вас скобочка вместо 0
Ответ дал:
0
AD = BC= 4 - Пифагоров треугольник 3 4 5
Высота пирамида = √(3^2-(5/2)^2)=√11/2
Пусть С - начало координат
Ось X- CB
Ось Y - CD
Ось Z - перпендикулярно АВС В сторону S
Вектор
SB(2;-3/2; -√11/2)
Плоскость СEF уравнение
ax+by+cz=0
Подставляем координаты точек
E(2.4;1.2;0)
2.4a+1.2b=0
и F(10/3;2.5;√11/6)
10a/3+2.5b+√11c/6=0
Пусть a = -1 Тогда b= 2 c= -10/√11
Уравнение
-x + 2y - 10z /√11 =0
Нормаль N(-1; 2 ; -10/√11)
произведение нормали на SB
N*SB = -2 - 3 +5 = 0 - перпендикулярны - значить прямая и плоскость параллельны.
Приложения:

Вас заинтересует
2 года назад
2 года назад
3 года назад
3 года назад
9 лет назад
9 лет назад