Question

ПОМОГИТЕ СРОЧНО!!!!!!!!!!!!!


1. Найдите значение выражения:

а). (16-13*6^2)^3 б). -5а^2


2. Выполните действия:

а). х^12*х^10
б). х^18:х^13
в). (х^2)^5
г). (ху)^7
д). (х3)^3


3. Запишите число 38000 в стандартном виде.


4. Упростите выражение:

а). -3а^5*4ав^6
б). (-2ху^6)^4
в). (-3а^3в^4)^3


5. Вычислите:

а). 6^15*6^116^24
б). 3^11*279^6


6. Упростите выражение:

а). -3 15а^8в*(12а^3в^8)^4
б). х^n-2*х^2*х^n+2

Answer 1

Нет желания расписывать тут полчаса. Все решения на прикреплённой фотке.

Возникли проблемы с заданием 1 - б и 6 - б. Возможно я что-то не так понял или ты написал непонятно либо неправильно.

Тут для решения нужно знать следующие фишки:

1) Если мы возводим число в какой-либо степени в степень, то нужно просто перемножить степени (пример 3 - в)

2) Если перемножаем (делим) числа в n степени с одинаковым основанием, то тогда мы просто переписываем основания и складываем (вычитаем) степени (пример 2 -а и 2-б)

В целом, 2-ое задание показывает необходимые операции на степенными числами.

к 3 заданию: стандартный вид числа выглядит примерно так "x.xxx*10^n". Т.е. 1 знак до запятой, какое-либо число знаков после запятой и умножаем всё это на 10 в нужной степени. Проанализируй 3 задание и поймёшь.

Удачи)

Answer 2

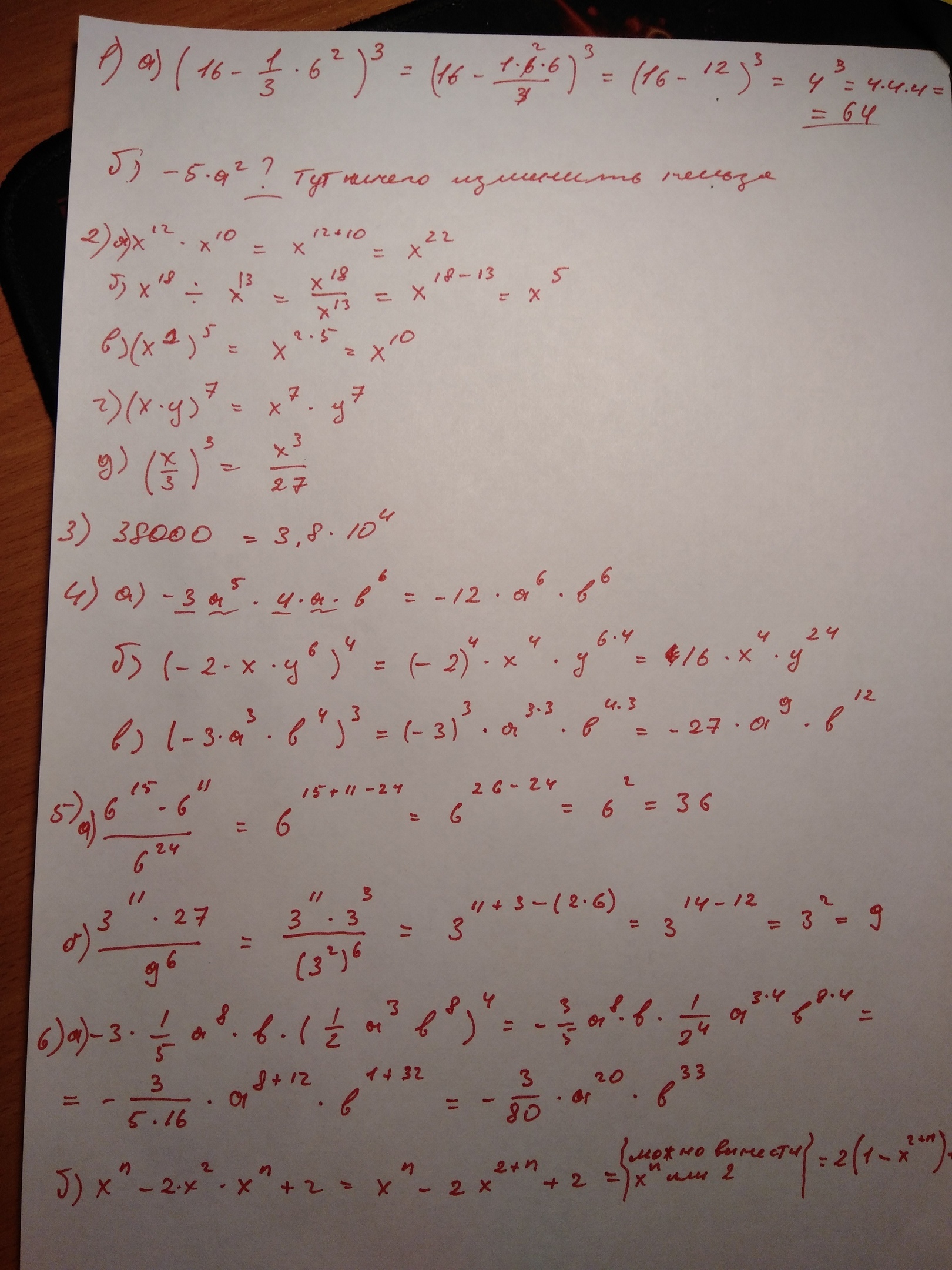
Ответ:

Объяснение:

$displaystyle 1.\ a) (16-frac 1 3 cdot 6^2)^3 = (16-12)^3 = 4^3 = 64$

б) -5a² можно дополнить этот пункт так: если $a = frac 2 5$

$-5a^2 = -5 cdot (frac 2 5)^2 = -5 cdot frac {4} {25} = -frac{4}{5} = -0.8$

$displaystyle 2. \ a)~ x^{12} cdot x^{10} = x^{12+10} = x^{22} \ \ b) ~x^{18} : x^{13} = x^{18-13} = x^5 \ \ c) ~(x^2)^5 = x^{2cdot 5} = x^{10} \ \ d) ~ (xcdot y)^7 = x^7 cdot y^7 \ \ e)~ bigg (frac x 3 bigg )^3 = frac{x^3}{3^3} = frac{x^3}{27}$

3.

Число записано в стандартном виде если оно записано в виде: a · 10ⁿ, где 1 ≤ a < 10 и n - целое число

$displaystyle 38000 = 3.8 cdot 10000= 3.8cdot 10^4$

$displaystyle 4. \ a) -3a^5cdot 4cdot a cdot b^6 = -3 cdot 4 cdot a^{5+1} cdot b^6 = -12 a^6 b^6 = -12(ab)^6 \ \ b) (-2cdot x cdot y^6)^4 = (-2)^4 cdot x^4 cdot y^{6cdot 4} = 16cdot x^4cdot y^{24} \ \ c) (-3cdot a^3 cdot b^4)^3 = (-3)^3 cdot a^{3 cdot 3} cdot b^{4cdot 3} = -27cdot a^9 cdot b^{12}$

$displaystyle 5. \ a) ~ frac{6^{15} cdot 6^{11}}{6^{24}} = frac{6^{15+11}}{6^{24}} = frac{6^{26}}{6^{24}} = 6^{26-24} = 6^2 = 36 \ \ b) ~ frac{3^{11}cdot 27}{9^6} = frac{3^{11}cdot 3^3}{(3^2)^6} = frac{3^{11+3}}{3^{2cdot 6}} = frac{3^{14}}{3^{12}} = 3^{14-12} = 3^2 = 9$

$displaystyle 6.\ a) ~ -3 frac 1 5 cdot a^8 cdot b cdot bigg (frac 1 2 cdot a^3 cdot b^8 bigg )^4 = -frac{16}{5} cdot a^8 cdot b cdot bigg (frac 1 2 bigg )^4 cdot a^{3cdot 4} cdot b^{8 cdot 4} = -frac{16}{5} cdot frac{1}{16} cdot a^{8+12} cdot b^{1+32} = \ \ = -frac 1 5 cdot a^{20} cdot b^{33} \ \ \ b) ~ x^{n-2} cdot x^2 cdot x^{n+2} = x^{n-2+2+n+2} = x^{2n+2} = x^{2(n+1)}} = (x^2)^{n+1}$