Ответы
Я вот решила , надеюсь помогла, если можешь помоги и мне
2. Исследовать функции на непрерывность.
3. Исследовать функцию на четность, нечетность.
4. Найти интервалы возрастания и убывания функции и точки ее
экстремума.
5. Найти интервалы выпуклости и вогнутости графика функции и
точки его перегиба.
6. Найти асимптоты графика функции.
7. Используя результаты пунктов 1 – 6 построить график функции.
Для уточнения вида кривой можно найти дополнительные точки графика.
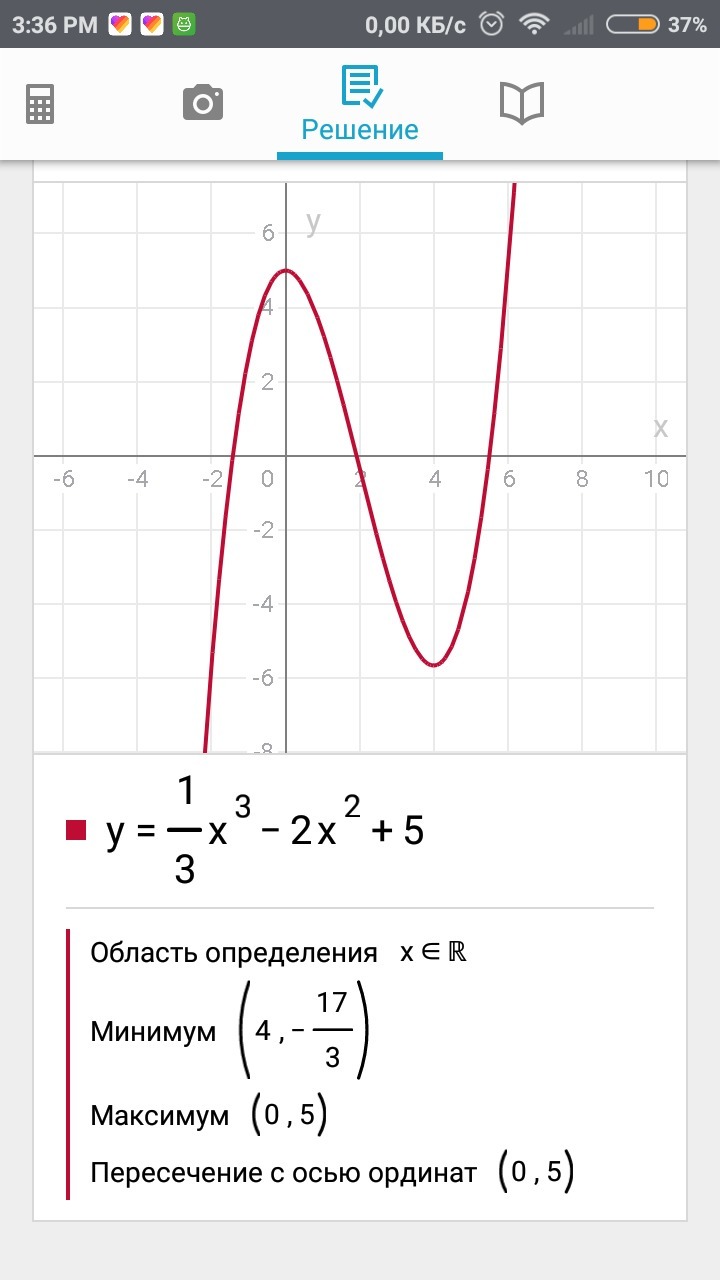
ДАНО: Y= 1/3*x³ - 2*x² + 5
ИССЛЕДОВАНИЕ.
1. Область определения D(x) - Х∈(-∞;+∞) - непрерывная.
2. Пересечение с осью Х. Y=0 при Х₁ = - 1,42, Х₂ = 1,92, Х₃ = 5,51 - без комментариев - просто верим на слово.
Положительна - X∈(Х₁;Х₂)∪(Х₃;+∞),
отрицательна - X∈(-∞;Х₁)∪(Х₂;Х₃).
3. Пересечение с осью У. У(0) = 5.
4. Поведение на бесконечности.limY(-∞) = - ∞ limY(+∞) = +∞
5. Исследование на чётность.Y(-x) ≠ Y(x). Y(-x) ≠ -Y(x), Функция ни чётная ни нечётная.
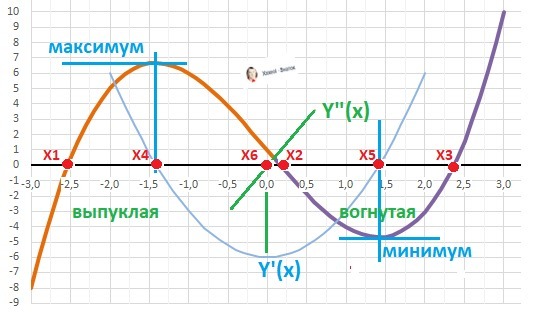
6. Производная функции.Y'(x)= x² -4*Х = x*(x-4) = 0.
Корни при Х₄= 0, Х₅ = 4 Схема знаков производной - положительная парабола - отрицательная между корнями.. (-∞)__(>0)__(Х₄)___(<0)___(Х₅)__(>0)_____(+∞)
7. Локальные экстремумы.
Максимум Ymax(Х₄)= 5 , минимум – Ymin(Х₅) = - 5 2/3 (≈-5,67).
8. Интервалы возрастания и убывания.
Возрастает - Х∈[-∞; Х₄]∪[Х₅;+∞), убывает = Х∈(Х₄; Х₅).
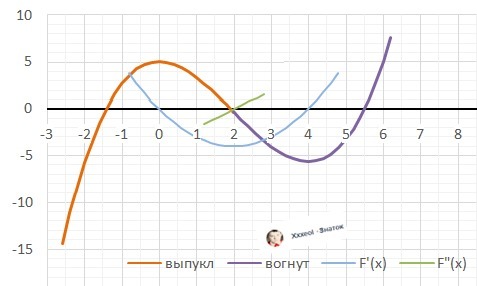
8. Вторая производная - Y"(x) = 2*x - 4=0.
Корень производной - точка перегиба Х₆= 2.
9. Выпуклая “горка» Х∈(-∞; Х₆).
Вогнутая – «ложка» Х∈(Х₆; +∞).
10. График в приложении.