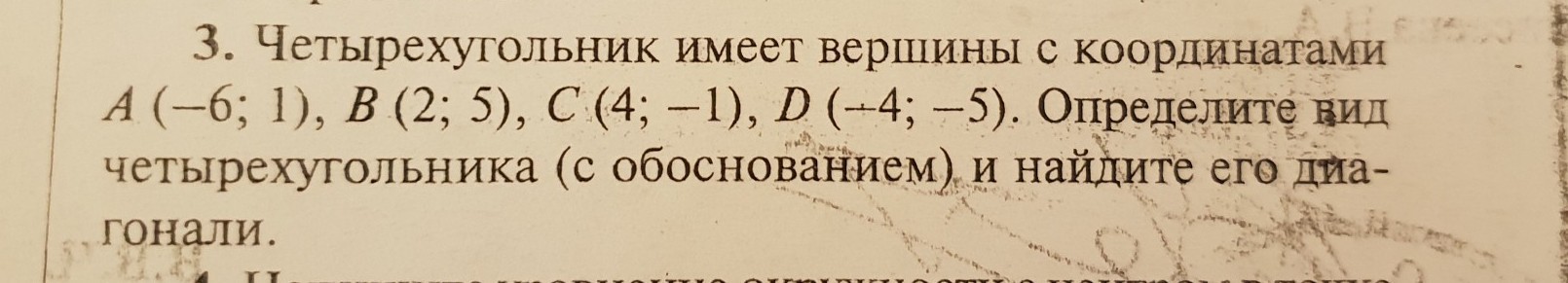Question

Алгебра, помогите, буду благодарен!

Answer 1

Найдем длины всех сторон четырехугольника

$|AB|=sqrt{(2+6)^2+(5-1)^2}=sqrt{80}\ |BC|=sqrt{(4-2)^2+(-1-5)^2}=sqrt{40}\ |CD|=sqrt{(-4-4)^2+(-5+1)^2}=sqrt{80}\ |AD|=sqrt{(-4+6)^2+(-5-1)^2}=sqrt{40}$

Так как противоположные стороны равны, то четырехугольник ABCD - параллелограмм.

Покажем, что ABCD - прямоугольник. Для этого достаточно найти угол между векторами AB, BC:

$overrightarrow{AB}={2+6;5-1}={8;4}\ overrightarrow{BC}={4-2;-1-5}={2;-6}$

$cos left(overrightarrow{AB},overrightarrow{BC}right)=dfrac{overrightarrow{AB}cdotoverrightarrow{BC}}{|overrightarrow{AB}|cdot|overrightarrow{BC}|}=dfrac{8cdot2+4cdot(-6)}{sqrt{80}cdotsqrt{40}}=dfrac{-8}{40sqrt{2}}=-dfrac{1}{5sqrt{2}}$

Угол между векторами AB и BC равен $arccos(-frac{1}{5sqrt{2}})approx98^circ$

Следовательно, ABCD не является прямоугольником, а значит является параллелограммом.

Найдем длины диагоналей параллелограмма:

$|AC|=sqrt{(4+6)^2+(-1-1)^2}=2sqrt{26}$

$|BD|=sqrt{(-4-2)^2+(-5-5)^2}=2sqrt{34}$