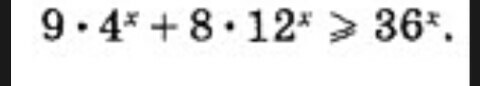Question

РЕШИТЕ НЕРАВЕНСТВО пожалуйста

Answer 1

$9cdot4^x+8cdot12^xgeq36^x\9cdot(2^x)^2+8cdot2^xcdot6^x-(6^x)^2geq0\9cdotdfrac{(2^x)^2}{(6^x)^2} +8cdotdfrac{2^xcdot6^x}{(6^x)^2} -dfrac{(6^x)^2}{(6^x)^2} geq0\9cdotleft(left(dfrac{1}{3}right)^xright)^2 +8cdotleft(dfrac{1}{3}right)^x -1 geq0$

Решим соответствующее уравнение:

$9cdotleft(left(dfrac{1}{3}right)^xright)^2 +8cdotleft(dfrac{1}{3}right)^x -1 =0\D_1=4^2-9cdot(-1)=25\left(dfrac{1}{3}right)^xneq dfrac{-4-5}{9} <0\\left(dfrac{1}{3}right)^x=dfrac{-4+5}{9} =dfrac{1}{9} =left(dfrac{1}{3}right)^2Rightarrow x=2$

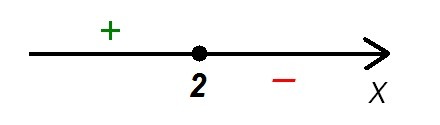
По методу интервалов найдем решение "больше нуля" (картинка). Правый интервал имеет знак "минус", поскольку основание показательной функции меньше 1.

$x leq 2$

Answer 2

а ответ какой?

Answer 3

x<=2

Answer 4

и какие промежутки?

Answer 5

Артем