Question

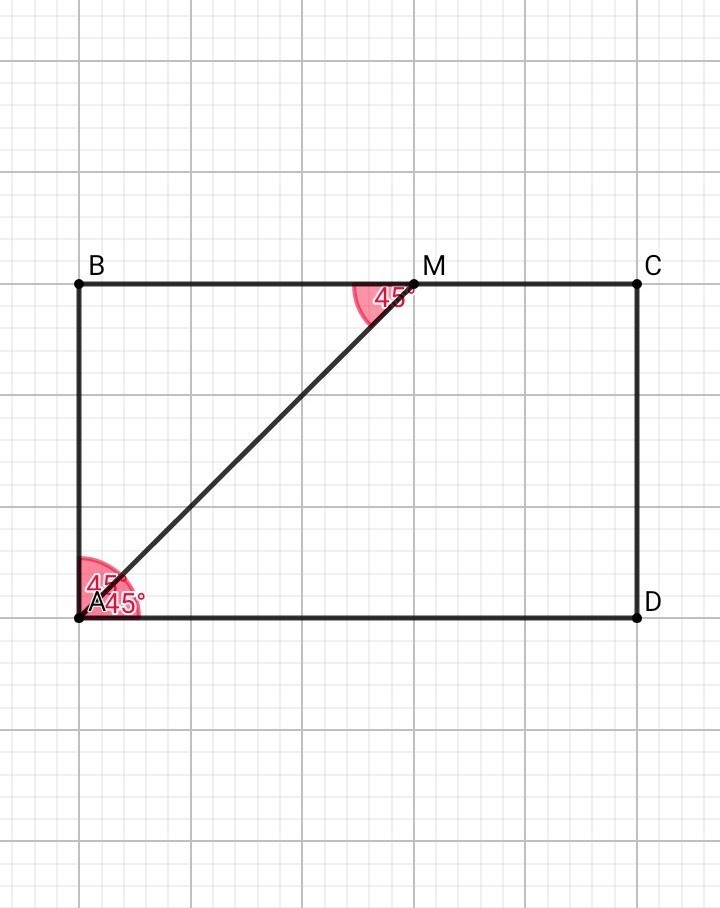
В прямоугольнике АБСД проведена биссектриса угла А, которая пересекает сторону ВС в точке М. Найти периметр прямоугольника, если ВМ=3см, СМ=2см

Answer 1

• АМ - биссектриса =>
угол ВАМ = угол САD = угол А / 2 = 90° / 2 = 45°
• Рассмотрим тр. АВМ:
Сумма острых углов в прямоугольном треугольнике равна 90°
угол ВАМ + угол ВМА = 90°
угол ВМА = 90° - 45° = 45°
Значит, тр. АВМ - прямоугольный и равнобедренный => АВ = ВМ = 3см
BC = BM + MC = 3 + 2 = 5 см
• Р abcd = 2 • ( AB + ВС ) = 2 • ( 3 + 5 ) = 2 • 8 = 16 см


ОТВЕТ: 16