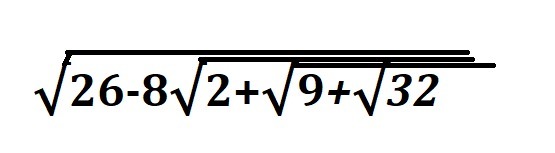Ответы
Ответ дал:
0
Полное решение и ответ находятся в прикрепленных материалах;
Добавил объяснение перехода в начале*
Добавил объяснение перехода в начале*
Приложения:

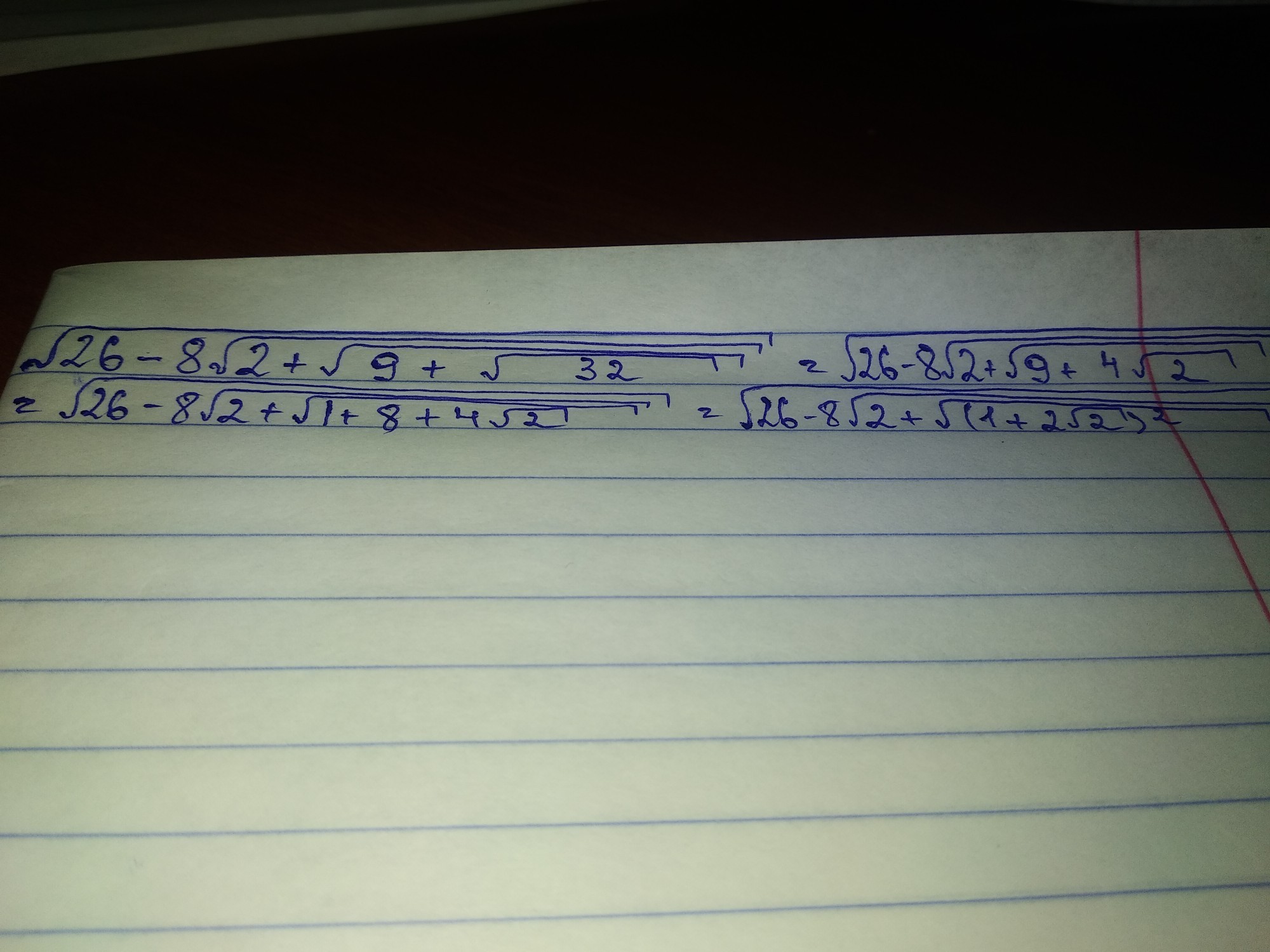
Ответ дал:
0
Разложение множителей*
Ответ дал:
0
9-ку разложил на 8 и 1 ? Это объясняет откуда в последствии появилась вторая восьмёрка.
Ответ дал:
0
Тут используется формула квадрата суммы
Ответ дал:
0
С какого разложения появилась единица?
Ответ дал:
0
9 представляешь в виде суммы 1 и 8 => 1+4√2+8
Ответ дал:
0
ОТВЕТ: 4 - V2
Приложения:

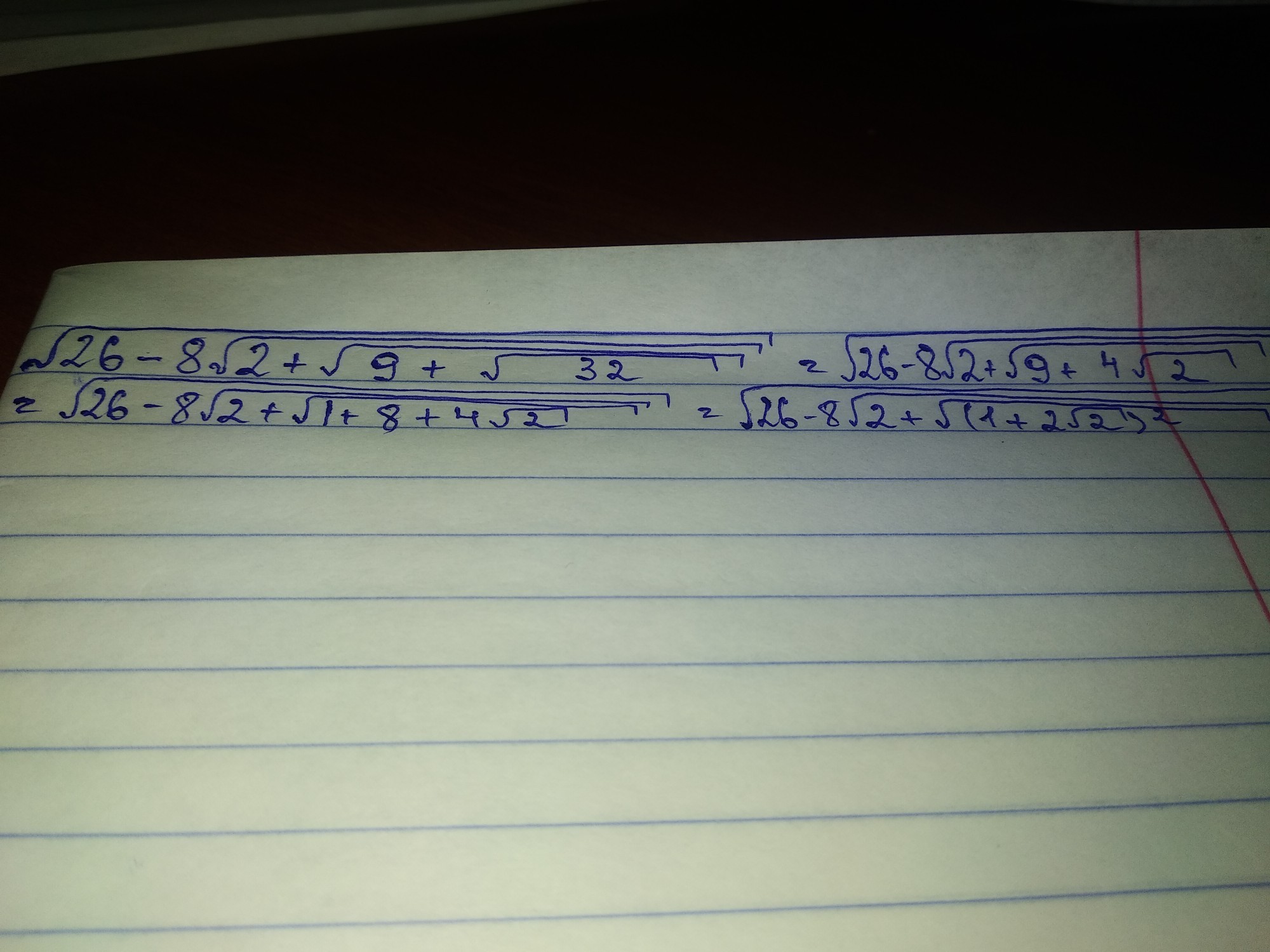
Ответ дал:
0
9 + V32 = 9 + 4V2 = 1 + 4V2 + 8 = 1^2 + 2•2V2 + ( 2V2 )^2 = ( 1 + 2V2 )^2 - квадрат суммы. Если пойти в обратную сторону, раскрыть скобку по формуле квадрата суммы, получите то же самое и т.д.
Ответ дал:
0
Где ты был минут десять назад?)))9)
Ответ дал:
0
:D
Вас заинтересует
2 года назад
3 года назад
3 года назад
9 лет назад
9 лет назад
10 лет назад
10 лет назад