1)Докажите неравенство.(номер 124 (а))
2)Докажите,что при любом значении а верно неравенство:(номер 125 (а))
Приложения:
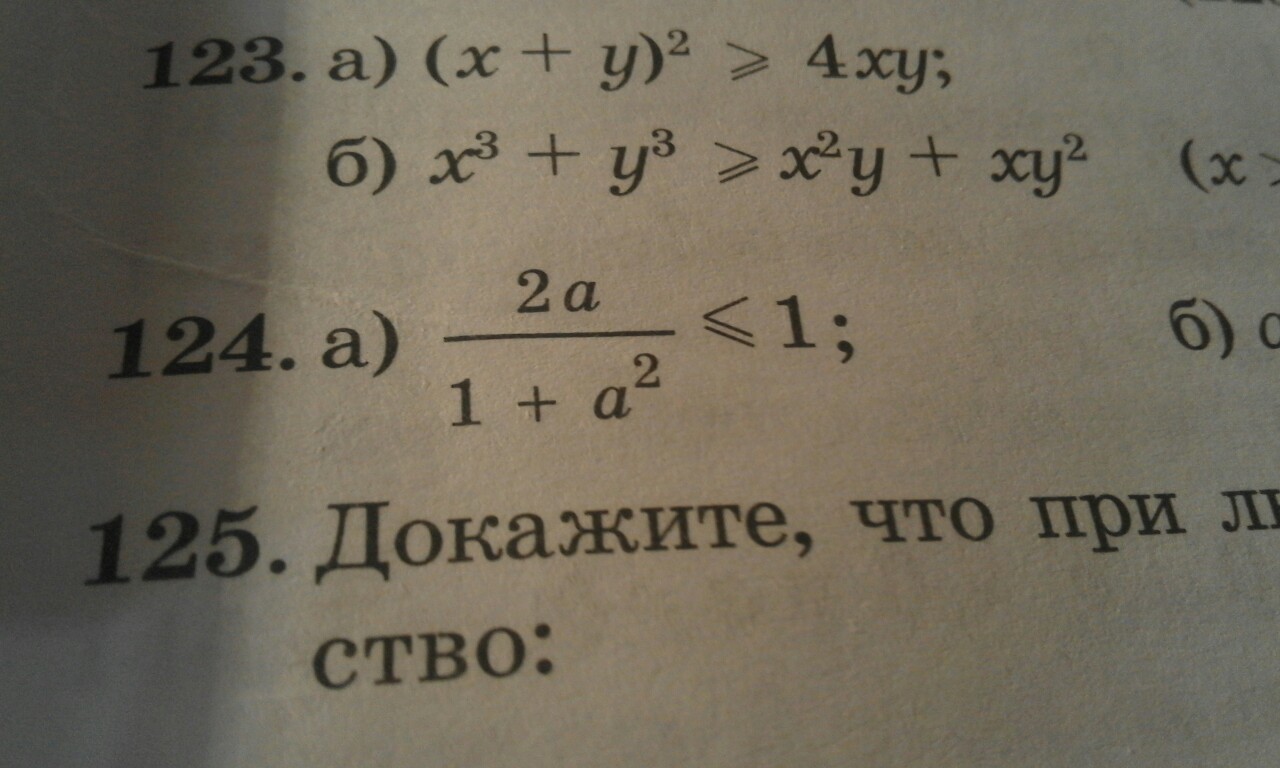
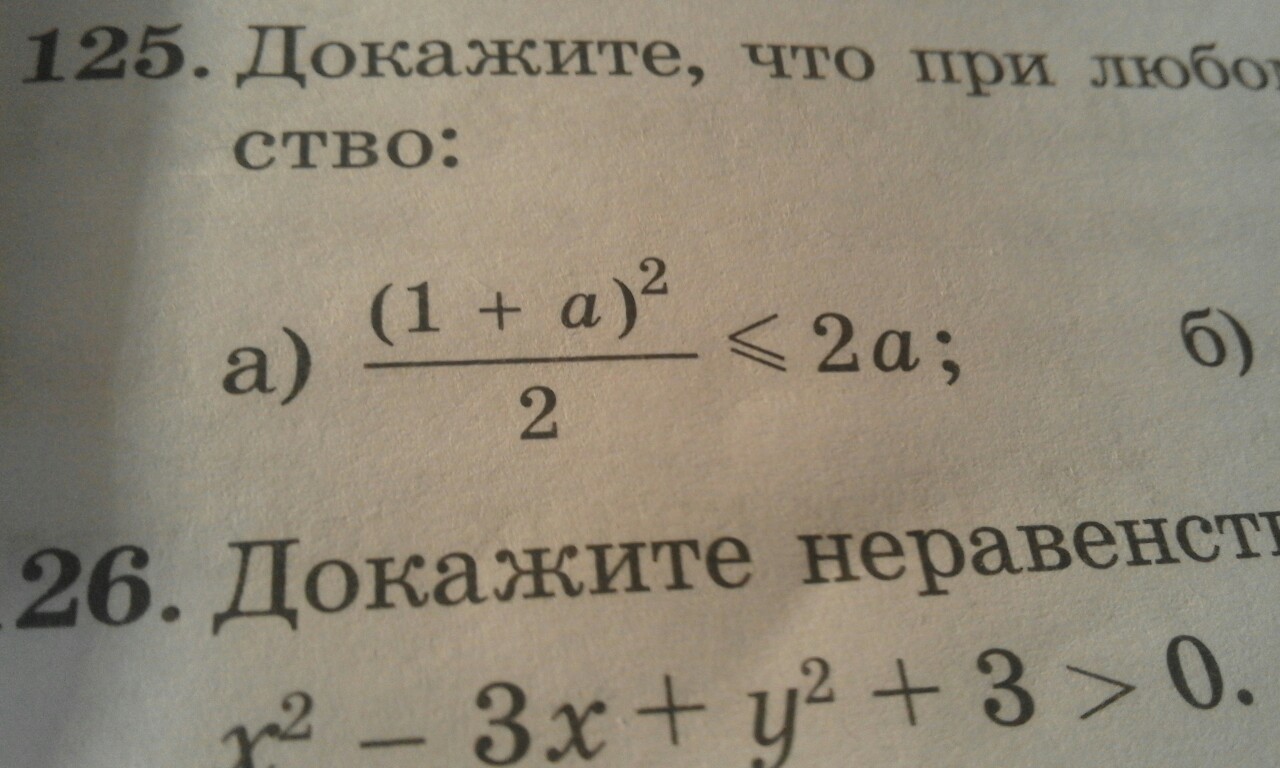
Ответы
Ответ дал:
0
#124: Доказать неравенство.
Знаменатель дроби всегда будет больше либо равен 0, так как любое число в квадрате неотрицательно, а если к неотрицательному числу прибавить 1, то получится положительное число.
Осталось доказать, что неотрицательным будет числитель.
Увидели формулу квадрата разности, свернули её. Получили верное для любого а неравенство, так как квадрат любого числа неотрицателен.
Доказано. ∎
#125: Доказать выполнение неравенства для любого значения a.
Квадрат числа не может быть меньше нуля, значит полученное неравенство можно переписать в равенство.
Таким образом, данное неравенство верно только для a = 1, а не для всех а.
Вывод: неравенство не выполняется для всех а.
Ответ дал:
0
Спасибо!
Вас заинтересует
2 года назад
3 года назад
3 года назад
9 лет назад
9 лет назад
10 лет назад