100 баллов!
Если основанием пирамиды есть треугольник со сторонами 4, 5 и 7см, а высота пирамиды равна наибольшей высоте основания, то чему равен объем пирамиды? Решение обязательно с рисунком
Ответы
Ответ дал:
0
Если основанием пирамиды есть треугольник со сторонами 4, 5 и 7см, а высота пирамиды равна наибольшей высоте основания, то чему равен объем пирамиды?
РЕШЕНИЕ:
• Рассмотрим тр. АВС:
По формуле Герона найдём площадь треугольника АВС:

где р = ( а + b + c ) / 2 - полупериметр, а, b и с - стороны треугольника

• Площадь треугольника АВС равна:
S abc = ( 1/2 ) • AC • h1
4V6 = ( 1/2 ) • 4 • h1
h1 = 2V6
• S abc = ( 1/2 ) • AB • h2
4V6 = ( 1/2 ) • 5 • h2
h2 = 8V6 / 5
• S abc = ( 1/2 ) • BC • h3
4V6 = ( 1/2 ) • 7 • h3
h3 = 8V6 / 7
Наибольшая высота треугольника АВС равна 2V6
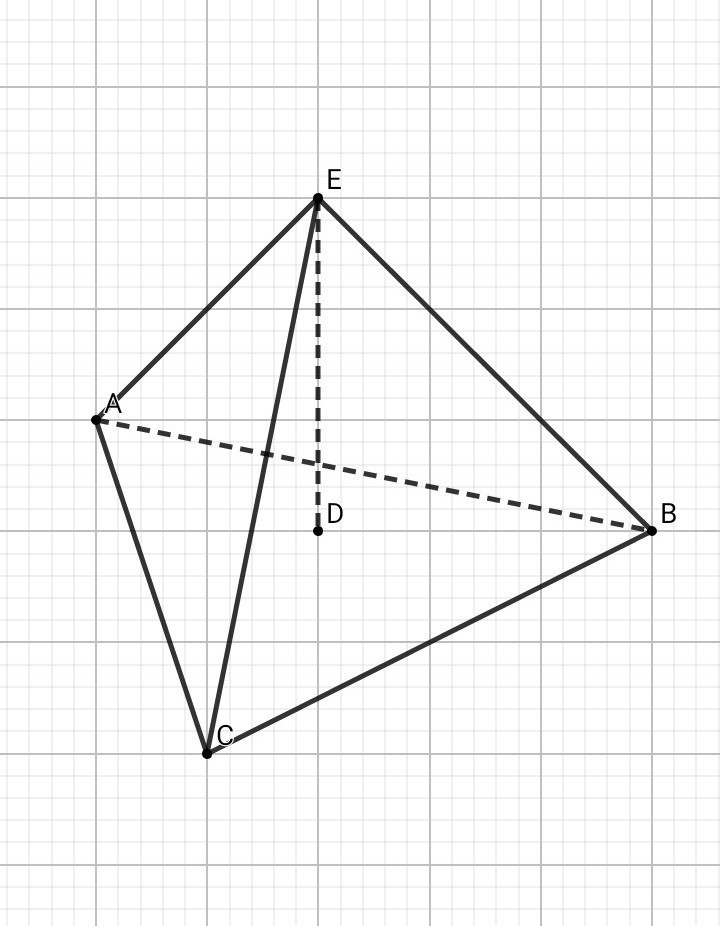
Значит, ED = 2V6
• Обьём пирамиды ЕАВС равен:
V = ( 1/3 ) • S abc • ED = ( 1/3 ) • 4V6 • 2V6 = 2 • 8 = 16
ОТВЕТ: 16
РЕШЕНИЕ:
• Рассмотрим тр. АВС:
По формуле Герона найдём площадь треугольника АВС:
где р = ( а + b + c ) / 2 - полупериметр, а, b и с - стороны треугольника
• Площадь треугольника АВС равна:
S abc = ( 1/2 ) • AC • h1
4V6 = ( 1/2 ) • 4 • h1
h1 = 2V6
• S abc = ( 1/2 ) • AB • h2
4V6 = ( 1/2 ) • 5 • h2
h2 = 8V6 / 5
• S abc = ( 1/2 ) • BC • h3
4V6 = ( 1/2 ) • 7 • h3
h3 = 8V6 / 7
Наибольшая высота треугольника АВС равна 2V6
Значит, ED = 2V6
• Обьём пирамиды ЕАВС равен:
V = ( 1/3 ) • S abc • ED = ( 1/3 ) • 4V6 • 2V6 = 2 • 8 = 16
ОТВЕТ: 16
Приложения:
Ответ дал:
0
дело не в сложности. просто в полноте использования известных свойств, правил и теорем.
Ответ дал:
0
Если автор вопроса знал бы эти известные свойства, правила и теоремы, то не задавал бы вопрос.
Ответ дал:
0
Вы правы. Но Вы, как Знаток, могли ему подсказать это свойство. И решение имело-бы более простой и понятный вид. Впрочем, как есть, так и есть... Удачи!
Ответ дал:
0
Где на рисунке h1, h2,h3?
Ответ дал:
0
Вначале Вы должны впомнить, как формулируется площадь треугольника.
Вас заинтересует
2 года назад
2 года назад
3 года назад
3 года назад
9 лет назад
9 лет назад
10 лет назад