Ответы
Ответ дал:
0
I hope this helps you
Приложения:
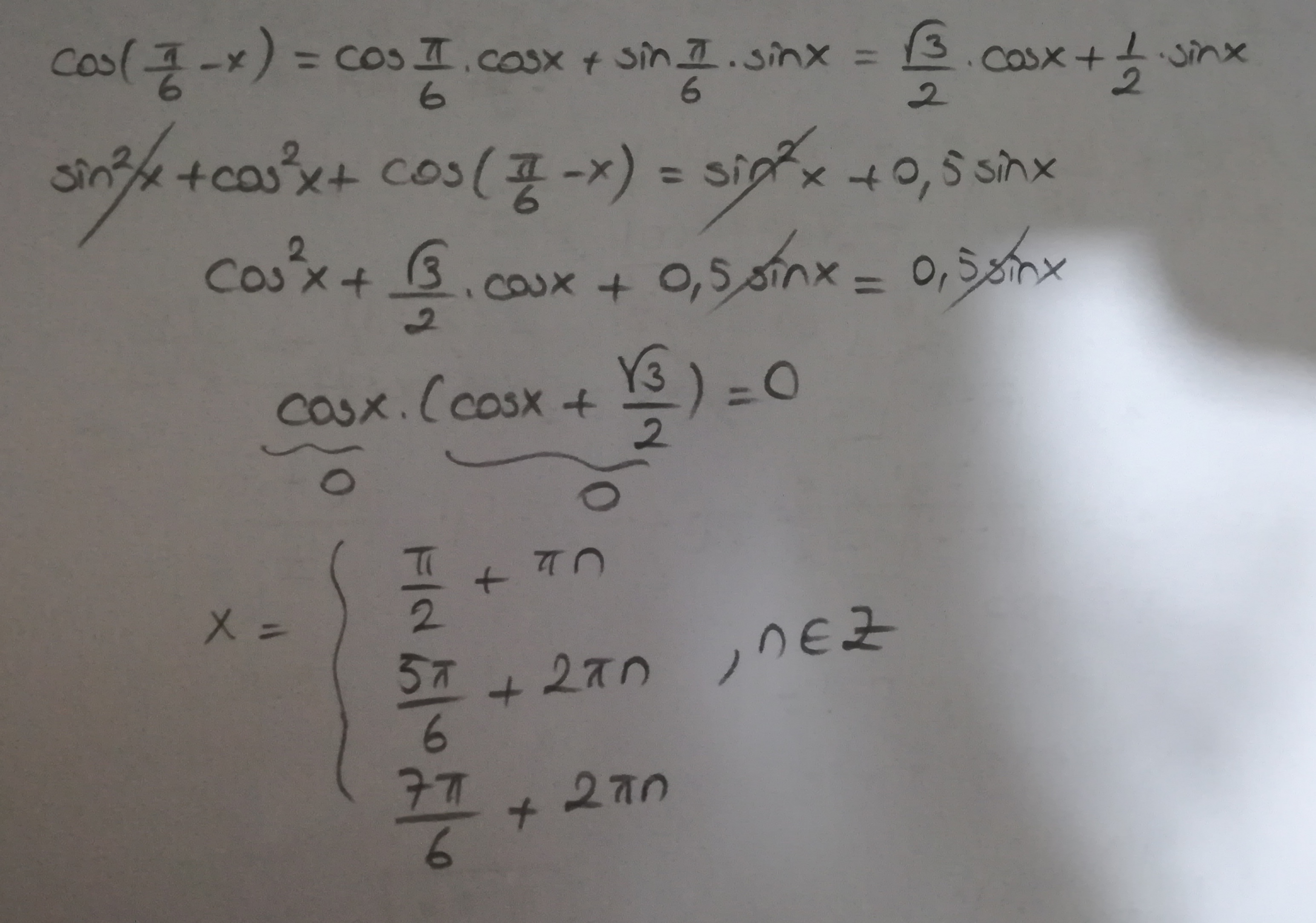
Ответ дал:
0
что то не понял куда единица делась в начале
Ответ дал:
0
ипать вас в лысину
Ответ дал:
0
отвечай нах
Ответ дал:
0
представили ее как cos^2x+sin^2x
Ответ дал:
0
Ответ:
Объяснение:
Ответ дал:
0
Ответ:
Объяснение:
1 + cos Π/6*cos x + sin Π/6*sin x = sin^2 x + 0,5*sin x
1 + √3/2*cos x + 0,5*sin x = sin^2 x + 0,5*sin x
1 + √3/2*cos x = sin^2 x
1 - sin^2 x + √3/2*cos x = 0
cos^2 x + √3/2*cos x = 0
cos x*(cos x + √3/2) = 0
1) cos x = 0
x1 = Π/2 + Π*k; k € Z
2) cos x = -√3/2
x2 = 5Π/6 + 2Π*n; n € Z
x3 = 7Π/6 + 2Π*n; n € Z
Вас заинтересует
2 года назад
3 года назад
9 лет назад
10 лет назад
10 лет назад