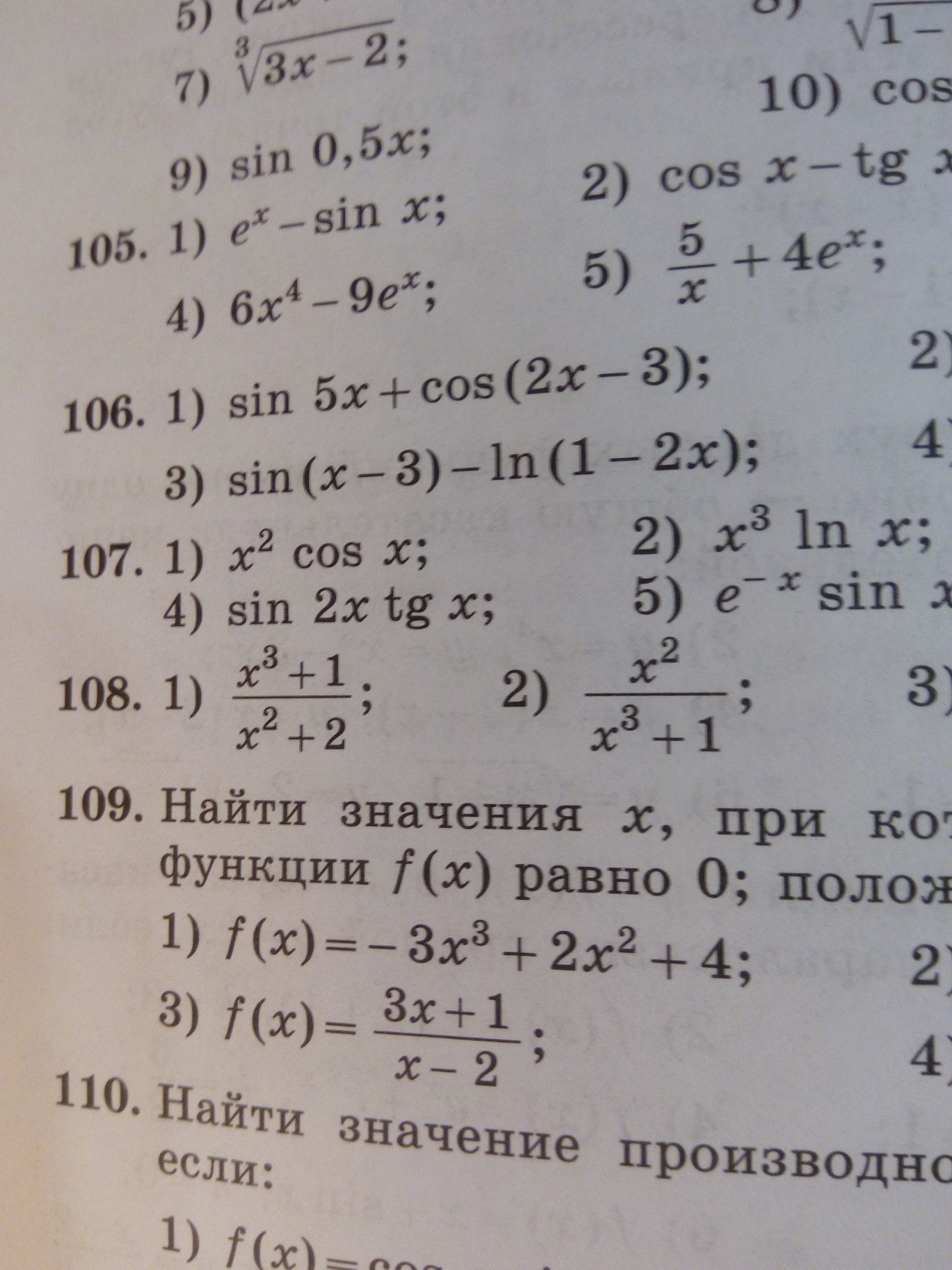Question

Срочно. Помогите пожалуйста. № 108(1,2) Найдите производную функции.

Answer 1

1). производная равна: 3x^2*(x^2+2)-(x^3+1)*2x / (x^2+2)^2=3x^4+6x^2-2x^4-2x /(x^2+2)^2=x^4+6x^2-2x / (x^2+2)^2.  2). производная равна: 2x*(x^3+1)-x^2*3x^2 / (x^3+1)^2=2x^4+2x-3x^4 / (x^3+1)^2=2x-x^4 / (x^3+1)^2.

Answer 2

первый пример не правильно, поменяйте, и применяйте Latex читать трудно.

Answer 3

$displaystyle y=frac{x^3+1}{x^2+2};\y'=frac{(x^3+1)'(x^2+2)-(x^3+1)(x^2+2)'}{(x^2+2)^2}=\frac{3x^2(x^2+2)-(x^3+1)2x}{(x^2+2)^2}=\frac{3x^4+6x^2-2x^4-2x}{(x^2+2)^2}=\frac{x^4+6x^2-2x}{(x^2+2)^2};$

$displaystyle y=frac{x^2}{x^3+1};\y'=frac{(x^2)'(x^3+1)-(x^2)(x^3+1)'}{(x^3+1)^2}=\=frac{2x(x^3+1)-(x^2)3x^2}{(x^3+1)^2}=\=frac{2x^4+2x-3x^4}{(x^3+1)^2}=\=frac{2x-x^4}{(x^3+1)^2};$