Question

Проекции двух сторон остроугольного
треугольника АВС
на прямую АС
имеют длины 6 см и 4 см. Какую длину имеют проекции медиан этого треугольника
на ту же прямую?

Answer 1

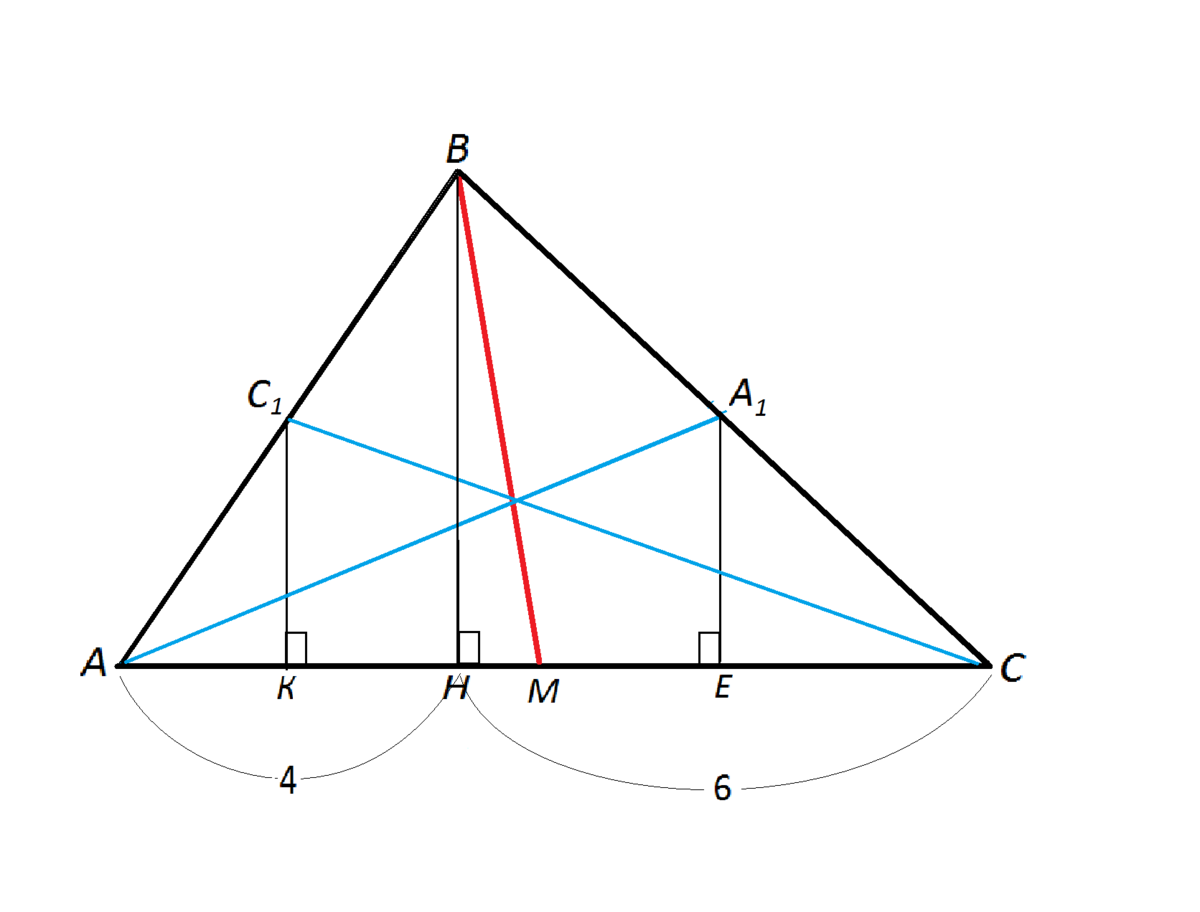
Сделаем рисунок.
Если из концов какого-нибудь наклонной опустим перпендикуляр на произвольную прямую, то отрезок прямой, заключённый  между основаниями наклонной и перпендикуляра, называется проекцией отрезка на эту прямую.
АН - проекция стороны АВ на АС. 
АН=4см
СН - проекция ВС на АС.
СН=6см
АС=4+6=10см
ВМ- медиана к АС
АМ=МС=10:2=5см
НМ - проекция ВМ на АС
НМ=АМ-АН=5-4=1см
СС1 -медиана к АВ
КС- проекция медианы СС1 на АС
КС=АС-АК
В треуголнике АВН отрезок С1К параллелен ВН. АС1=ВС1
С1К -  средняя линия треугольника АВН
АК=КН=4:2=2см
КС=10-2=8см
АА1 медиана к ВС
А1Е - средняя линия треугольника ВСН
НЕ=СН:2=3см
АЕ-проекция АА1 на АС
АЕ=АН+НЕ=4+3=7см
Ответ:
Проекция АА1=7см
проекция ВМ=1см
проекция СС1=8см