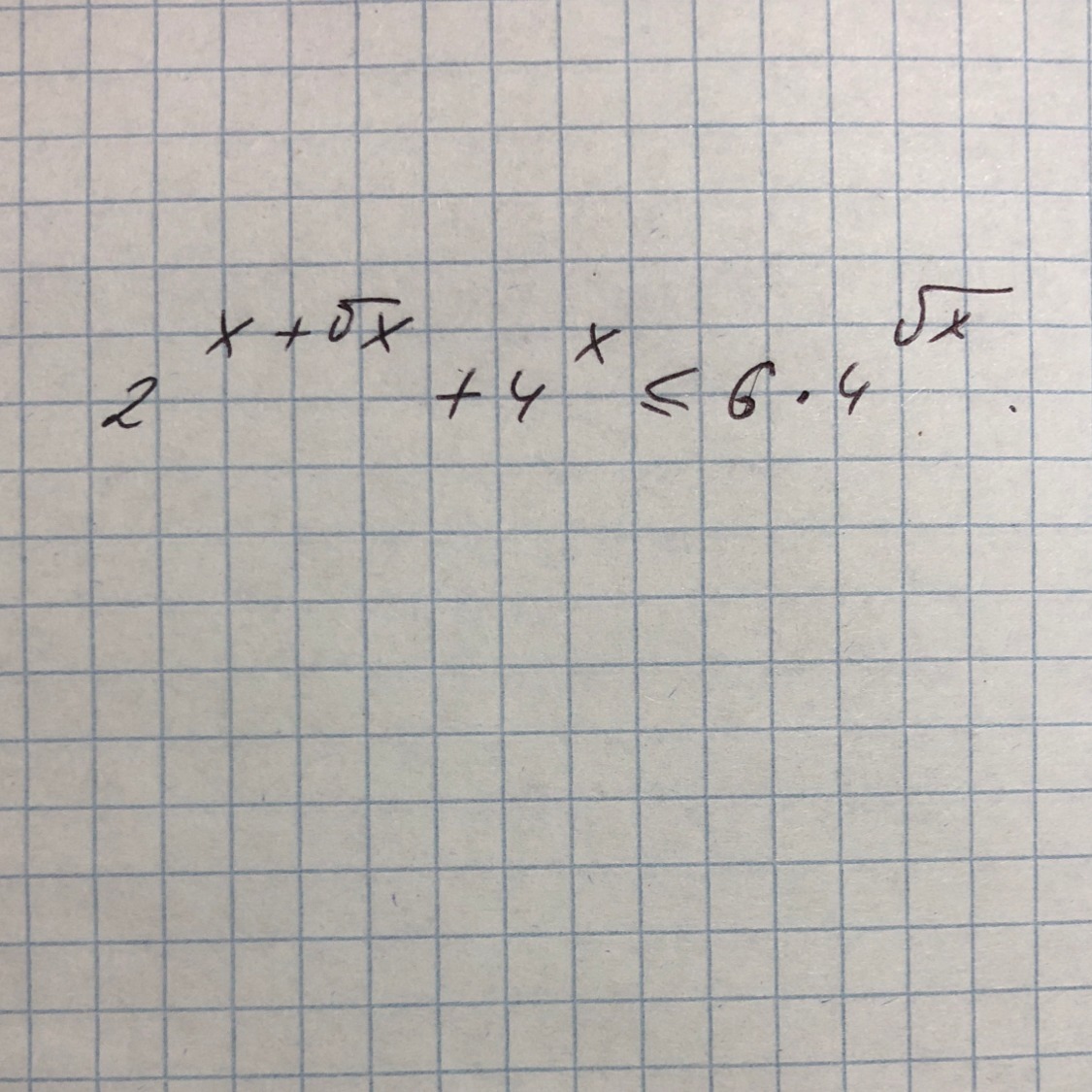Question

Решите, пожалуйста, показательное неравенство. Очень срочно

Answer 1

Неравенство равносильно неравенству

$2^x*2^{sqrt{x}}+(2^x)^2leq6*(2^{sqrt{x}})^2$

Пусть $2^x=a, 2^{sqrt{x}}=b, a>0, b>0$

$ab+a^2leq6b^2\a^2+ab-6b^2leq0\a^2+3ab-2ab-6b^2leq0\a(a+3b)-2b(a+3b)leq0\(a+3b)(a-2b)leq0$

I случай:

$begin{equation*}begin{cases}a+3bleq0\a-2bgeq0 end{cases}end{equation*}Rightarrow begin{equation*}begin{cases} aleq-3b\ageq2b end{cases}end{equation*}$

Так как b > 0, -3b < 0 ⇒ a < 0, но a > 0 - противоречие, значит, неравенство не имеет решений, следовательно, и система тоже не имеет решений.

II случай:

$begin{equation*}begin{cases}a+3bgeq0\a-2bleq0 end{cases}end{equation*}Rightarrowbegin{equation*}begin{cases}ageq-3b\aleq2b end{cases}end{equation*}Rightarrowbegin{equation*}begin{cases}frac{a}{b}geq-3\frac{a}{b}leq2 end{cases}end{equation*}Rightarrowbegin{equation*}begin{cases}frac{2^x}{2^{sqrt{x}}}geq-3\frac{2^x}{2^{sqrt{x}}}leq2 end{cases}end{equation*}Rightarrow$

$Rightarrow begin{equation*}begin{cases}2^{x-sqrt{x}}geq-3\ 2^{x-sqrt{x}}leq2^1 end{cases}end{equation*}Rightarrow x-sqrt{x}leq1 Leftrightarrow sqrt{x}geq x-1$

Если x < 1, то x ∈ [0; 1). Если x ≥ 1:

$xgeq x^2-2x+1\x^2-3x+1leq0\x^2-3x+1=0\x=frac{3pmsqrt{5}}{2} \ xin[frac{3-sqrt{5}}{2}; frac{3+sqrt{5}}{2}]$

Так как $frac{3-sqrt{5}}{2}<1$, решением данного случая будет $[1; frac{3+sqrt{5}}{2}]$

Объединим и получим ответ.

Ответ: $[0; frac{3+sqrt{5}}{2}]$