Question

ABCD прямоугольная трапеция. Угол C=150 градусов.найдите длину AB, если известно, что CD=14см

Answer 1

проведем перпендикуляр CF
по свойству катета лежащего против угла в 30° получаем что CF =1/2CD
BC || AD так как ABCD трапеция и по её свойству её основания параллельны
так как у нас прямоугольная трапеция то AB это перпендикуляр проведенный к основанию AD ,но так как CF так же перпендикуляр проведенный к основанию AD то AD || CF значит они равны
то есть длина перпендикуляра равна 7 так как CF лежит против угла в 30° а гипотинуза равна 14.
Ответ:2)7см.

Answer 2

Ответ:    7 см

Объяснение:

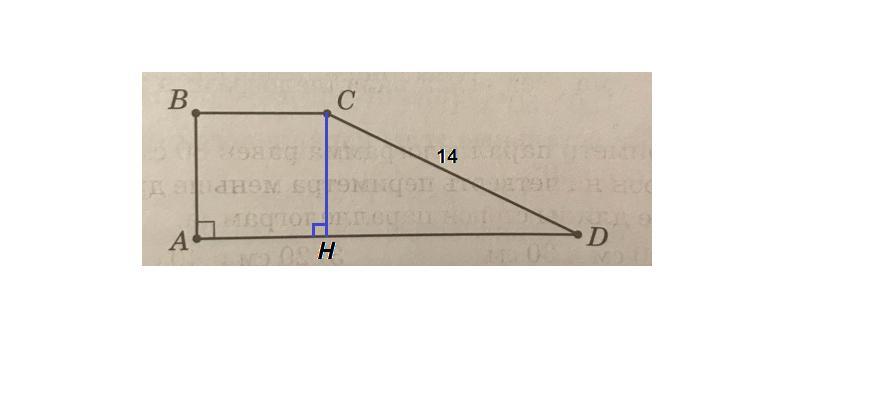
Сумма углов, прилежащих к боковой стороне трапеции, равна 180°, значит ∠D = 180° - ∠С = 180° - 150° = 30°.

Проведем высоту СН.

ΔCHD:  ∠CHD = 90°,  ∠CDH = 30°, ⇒

            CH = 1/2 CD = 1/2 · 14 = 7 см по свойству катета, лежащего напротив угла в 30°.

АВСН - прямоугольник, так как все его углы прямые, значит

АВ = СН = 7 см