Question

Найти максимум функции y=x^2-34x+144lnx+6

Answer 1

Найдём производную функции:

$y'=(x^2-34x+144ln{x}+6)'=(x^2)'+(-34x)'+(144ln{x})'+(6)'=\=2x-34+frac{144}{x}=frac{2x^2-34x+144}{x}=frac{2(x-8)(x-9)}{x}$

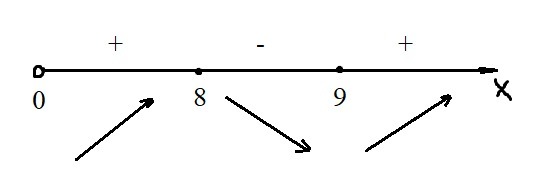
Посмотрим, как ведёт себя функция (см. рис.). Видно, что возрастание сменяется убыванием в точке x = 8. Значение в точке максимума: $8^2-34*8+144ln{8}+6=432ln{2}-202$

Ответ: $432ln{2}-202$