Ответы
Ответ дал:
0
Пусть . Тогда
Заменим a + b на c:
Заметим, что x = 1 - корень уравнения. Тогда разделим на
(см. картинку). Получим
. Тогда уравнение будет иметь вид:
Так как производилась замена a + b на c, могли появиться посторонние корни. Сделаем проверку:
x = -6:
Равенство не выполнилось - корень не подходит.
x = 1:
Равенство выполнилось - корень подходит.
Ответ: 1
Приложения:
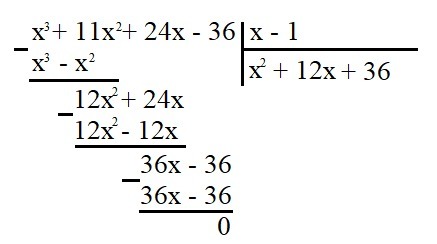
Ответ дал:
0
Он сам ее придумал. Доказательство довольно простое, Вы можете попробовать его придумать.
Ответ дал:
0
Кстати, я не понял, что Вы изменили в решении
Ответ дал:
0
>Так как производилась замена a + b на c, могли появиться посторонние корни. Сделаем проверку:
Ответ дал:
0
Понял. Спасибо за беседу. А сейчас пора и на боковую. Спокойной ночи
Ответ дал:
0
И Вам спокойной ночи.
Вас заинтересует
3 года назад
3 года назад
10 лет назад