Четырехзначное число начинается с цифры 4. Эту цифру переставили в конец числа. Полученное число оказалось на 1071 меньше исходного. Какова сумма цифр этого числа?
Ответы
Ответ дал:
0
________________________________
Приложения:
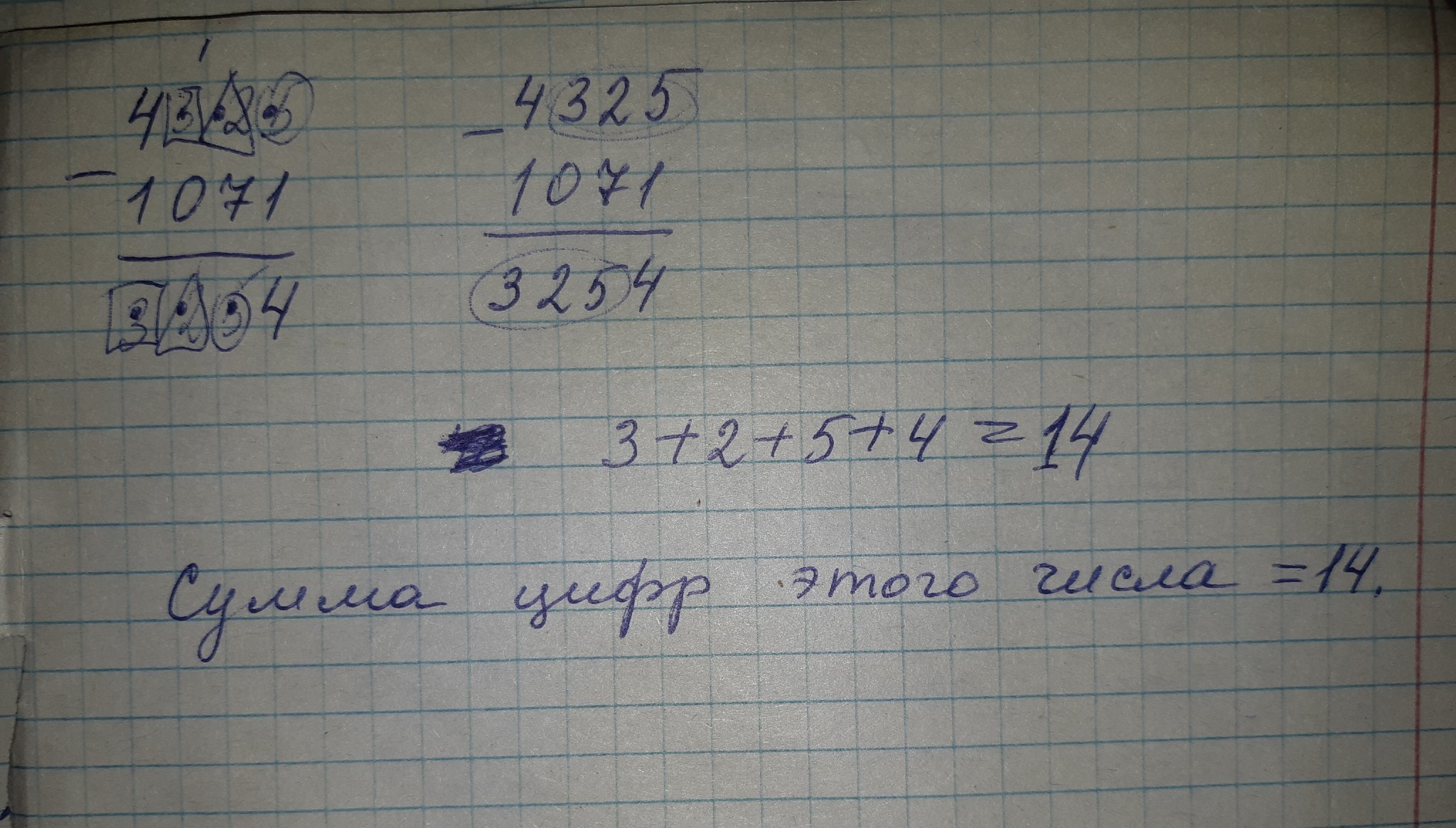
Ответ дал:
0
Речь идет только о волшебном числе = 9 - только от него сумма цифр не меняется.
Ответ дал:
0
В задаче 4325 - 3254 = 1071 суммы цифр 14 14 9 - так что это значит?
Ответ дал:
0
кстати, да. "если у разности сумма чисел=9, то и у исходного была 9" пример: 9443-6230=3213 ; 9257-3245=6012. Разность действительно в сумме 9, но ни у уменьшаемого, ни у вычитаемого в сумме 9 не получается. Это что за такое "волшебное правило с девяткой" ??? Если неправильно - просто удалите моё решение! Но с "волшебной" девяткой я не согласна.
Ответ дал:
0
Решение в общем виде: x-y=1071 ; y=(x-4000)*10-4 ; x-y=x-10x+40000-4=1071 ; 9x=40000-4-1071 ; 9x=38925 ; x=4325 ; y=3254 ; сумма цифр этого числа 14
Ответ дал:
0
исправить y=(x-4000)*10+4 (+перед 4)
Ответ дал:
0
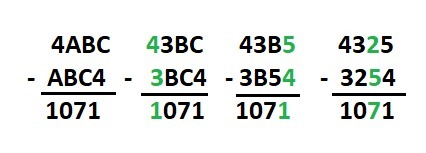
Неизвестные цифры обозначим буквами и запишем задачу в виде:
4АВС - АВС4 = 1071.
На рисунке в приложении решение "в столбик".
А = 4 -1 = 3 и С = 4 + 1 = 5 и В = 7 + С = 7 + 5 = 12 - 10 = 2.
Получили число 4325 и сумма его цифр:
4+3+2+5 = 14 и еще раз суммируем: 1 + 4 = 5.
ОТВЕТ: Сумма цифр - 5.
Приложения:
Ответ дал:
0
Вот это действительно НЕ ТАК! А сами числа то какие?
Ответ дал:
0
Добрый день! Поможете по физике? С УВ!
Ответ дал:
0
https://znanija.com/task/30479512
Вас заинтересует
3 года назад
3 года назад
10 лет назад