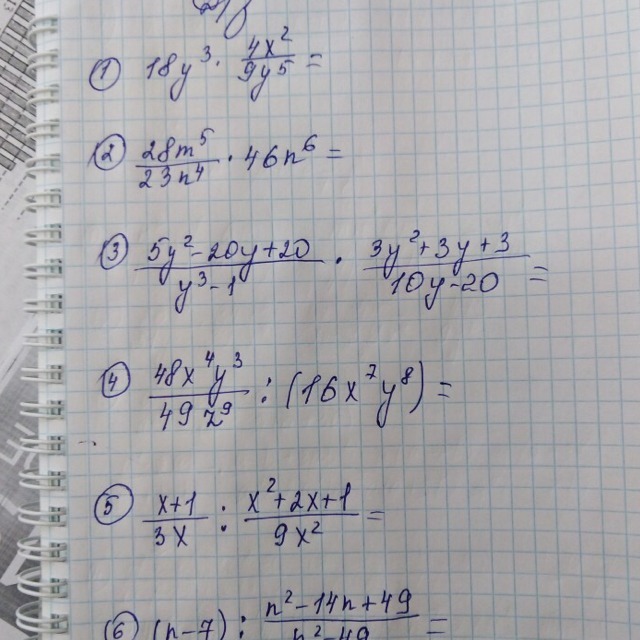Question

Помогите прошу, умоляю по человечески! Нужно выполнить умножение-деление

Answer 1

1) $frac{18y^3}{1} * frac{4x^2}{9y^5} = 2y^8 * 4x^2$

2) $frac{28m^5}{23n^4} * frac{46n^6}{1} = 28m^5 * 2n^10$

3) $frac{5y^2-20y+20}{y^3-1} * frac{3y^2+3y+3}{10y-20} = frac{y-2}{y^3-1} * frac{1}{10y-20} = 10y^2-40y-40 * y^3-1 = y-1 * y^3-1 = y^4$

Находим дискриминант:

1. 5y^2-20y+20 = 0

D = b^2-4ac = (-20)^2-4*5*20 = 400 - 400 = 0=0, 1 корень.

y = $frac{-b+-sqrt{D}} {2a}$

y₁ = $frac{20}{10} = 2$

2. 3y^2+3y+3 = 0

D = b^2-4ac = 3^2-4*3*3 = 9 - 36 = -25 < 0, нет корней.

Находим последний возможный дискриминант:

3. 10y^2-40y+40 = 0

D = b^2-4ac = (-40)^2 - 4*10*40 = 1600 - 1600 = 0 = 0, 1 корень.

y = $frac{20}{20} = 1$

4) $frac{48x^4y^3}{49z^9} : frac{16x^7y^8}{1} = frac{48x^4y^3}{49z^9} * frac{1}{16x^7y^8} =  frac{3x^11y^11}{49z^9}$

5) $frac{x+1}{3x} : frac{x^2+2x+1}{9x^2} = frac{x+1}{3x} : frac{x-1}{9x^2} = frac{x+1}{3x} * frac{9x^2}{x-1} = frac{x+1}{1} * frac{3x^3}{x-1} = x^2+1 * 3x^3 = 3x^5+1$

Находим дискриминант:

1. x^2+2x+1 = 0

D = b^2-4ac = 2^2-4*1*1 = 4-4 = 0=0, 1 корень.

x = $frac{2}{2} = 1$

6) $frac{n-7}{1} : frac{n^2-14n+49}{n^2-49} = frac{n-7}{1} * frac{n^2-49}{n-7} = n^2-49 = (n-7)(n+7)$

Находим дискриминант:

1. n^2-14n+49 = 0

D = b^2-4ac = (-14)^2 - 4*1*49 = 196 - 196 = 0=0, 1 корень.

n = $frac{14}{2} = 7$