СРОЧНО! Баллами не обижу! Исследовать график функции на:
-парность/непарность
-точки разрыва
-асимптоты
-нули функции
-экстремум
-точки перегиба
-монотонность
Приложения:
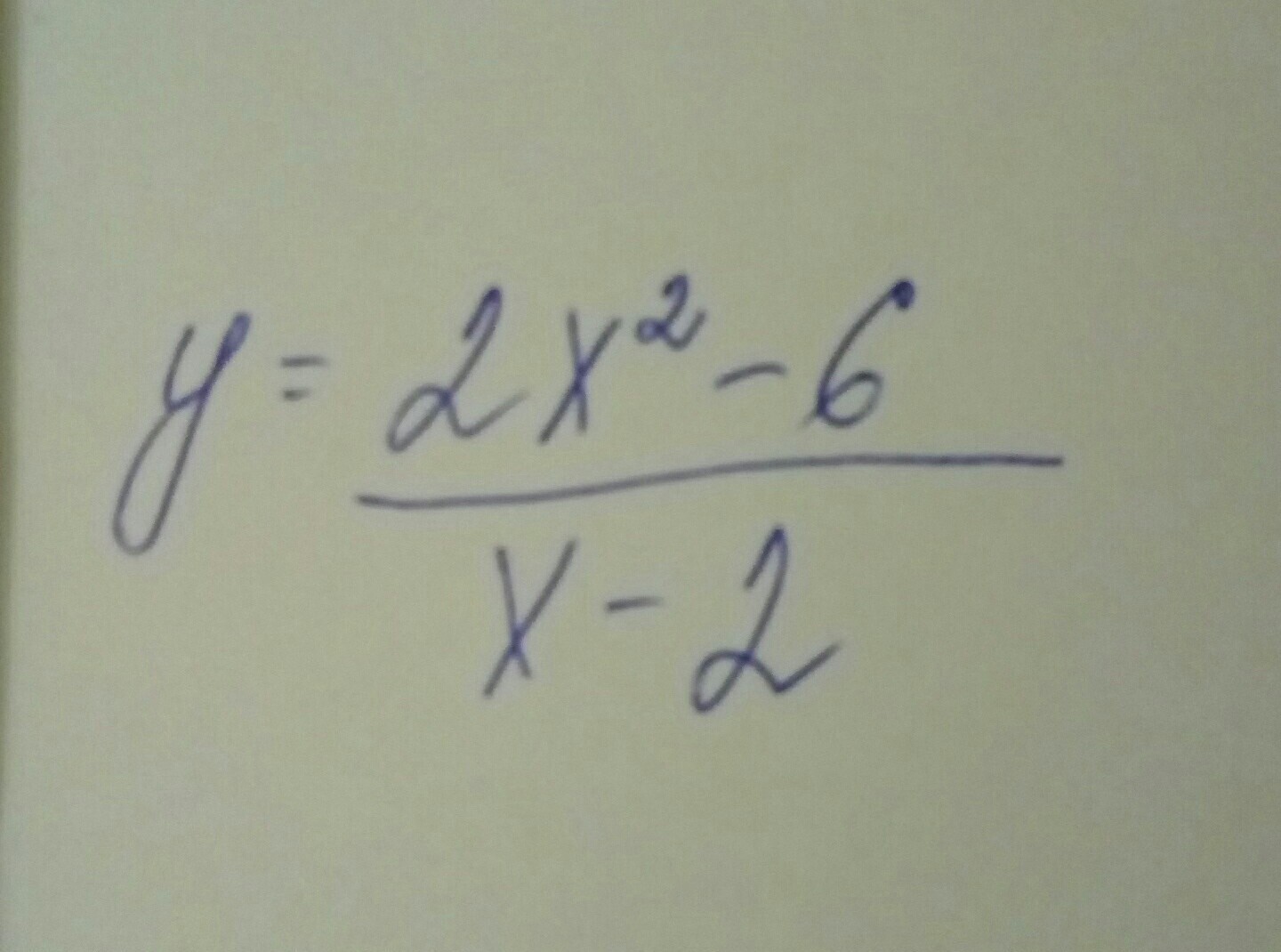
Ответы
Ответ дал:
0
Функция общего вида (не явл. ни чётной, ни нечётной).
2) Точка разрыва 2 рода: х=2, так как
Точек перегиба нет. На обл. определения ф-ция всюду вогнута.
Ответ дал:
0
https://znanija.com/task/9534886
Вас заинтересует
3 года назад
3 года назад
9 лет назад
10 лет назад
10 лет назад