Question

В равнобедренном треугольнике SAD с основанием SD на медиане AK отмечена точка L. Докажите, что треугольник SLA-равнобедренный. (по возможности с чертежом плиз)

Answer 1

Т.к. SAD - равнобедренный, то медиана АК является также высотой треугольника ⇒∠SKA=∠LKD=90°

SK=KD (так как медиана делит SD пополам),  LK - общая сторона, ∠SKA=∠LKD ⇒ ΔSKA=ΔLKD по первому признаку равенства треугольников (по двум сторонам и углу между ними) ⇒ SL=LD ⇒

SLD - равнобедренный.

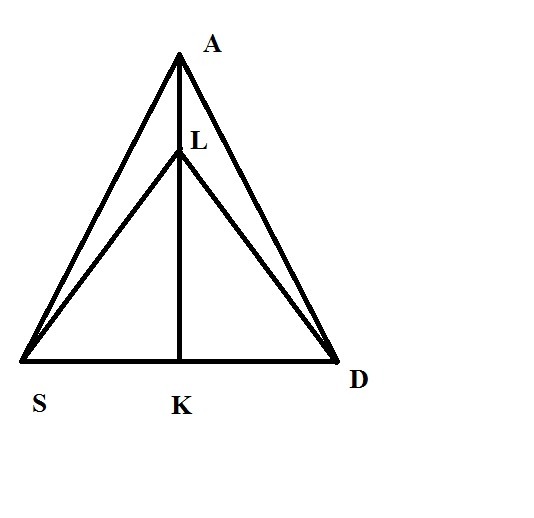
Δ SLA может быть равнобедренным, но это частный случай и из условий задачи это не следует. Как мы видим на чертеже, соответствующем условиям задачи, треугольник SLA не равнобедренный.

Answer 2

как SKA может быть равно LKD