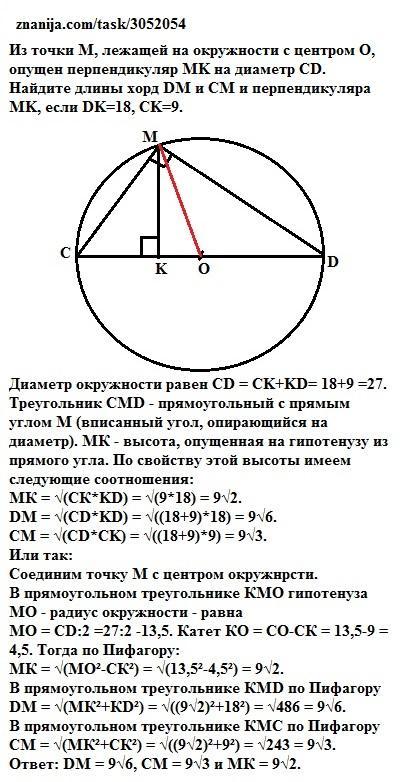
из точки M,лежащей на окружности с центром O,опущен перпендикуляр MK на диаметр CD.1)Найдите длины хорд DM и CM и перпендикуляра MK,если:DK=18,CK=9....
Ответы
Диаметр окружности равен CD = CK+KD= 18+9 =27. Треугольник СМD - прямоугольный с прямым углом М (вписанный угол, опирающийся на диаметр). МК - высота, опущенная на гипотенузу из прямого угла. По свойству этой высоты имеем следующие соотношения:
МК = √(СК*KD) = √(9*18) = 9√2.
DM = √(СD*KD) = √((18+9)*18) = 9√6.
CM = √(СD*CK) = √((18+9)*9) = 9√3.
Или так:
Соединим точку М с центром окружнрсти.
В прямоугольном треугольнике КМО гипотенуза МО - радиус окружности - равна
МО = CD:2 =27:2 -13,5. Катет КО = СО-СК = 13,5-9 =4,5. Тогда по Пифагору:
МК = √(МО²-СК²) = √(13,5²-4,5²) = 9√2.
В прямоугольном треугольнике КМD по Пифагору
DM = √(МК²+КD²) = √((9√2)²+18²) = √486 = 9√6.
В прямоугольном треугольнике КМС по Пифагору
CM = √(МК²+СК²) = √((9√2)²+9²) = √243 = 9√3.
Ответ: DM = 9√6, СМ = 9√3 и МК = 9√2.