Обясните пожалуйста решение неравенства методом интервалов, пожалуйста очень подробно
|2x-1|-|3x+1|≤0
Должно получится (-∞;-2)U(0;+∞)
Я пытался но неполучилось...
Приложения:
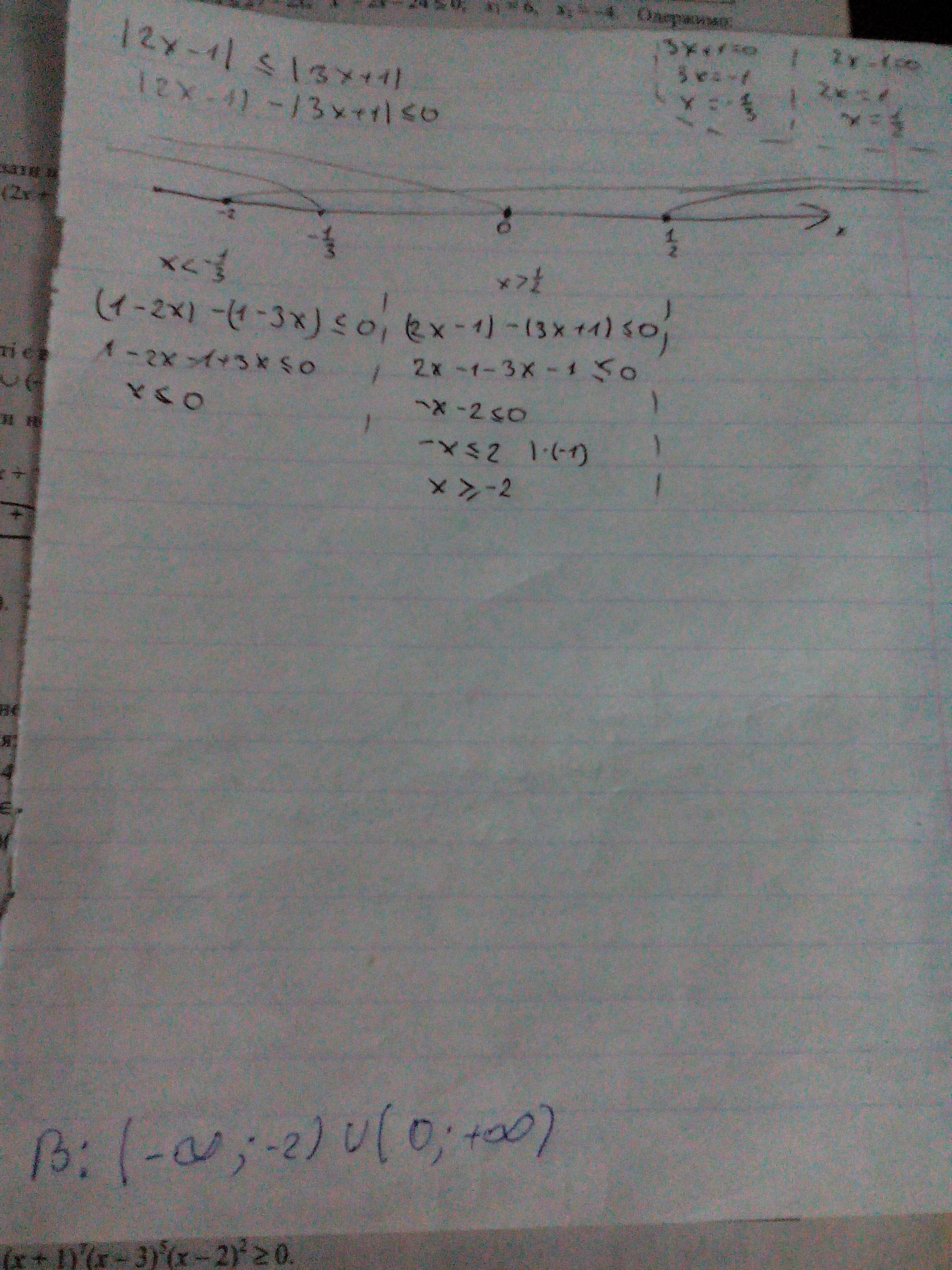
Ответы
Ответ дал:
0
т.к. обе части неравенства точно неотрицательны (по свойству модуля), то можно возвести обе части неравенства в квадрат и решить обычным методом интервалов. Еще придется применить формулу разности квадратов. Неравенство нестрогое, поэтому точки будут не выколотые.
+ - +
----------------- -2 ----------------------0----------------->x
Ответ: (-∞; -2] ∪ [0; +∞)
____________________________________________
Ответ дал:
0
Вы начали верно, рисунок, три участка. Далее нужно было правильно раскрыть модуль. Решение задания приложено.
Приложения:

Вас заинтересует
2 года назад
2 года назад
3 года назад
3 года назад
9 лет назад
9 лет назад
10 лет назад
10 лет назад