Question

Периметр правильного треугольника равен 24см. Вычислите радиус окружности описанной около этого треугольника и диаметр окружности, вписанной в него

Answer 1

1) а = 24 : 3 = 8 см -  сторона треугольника.

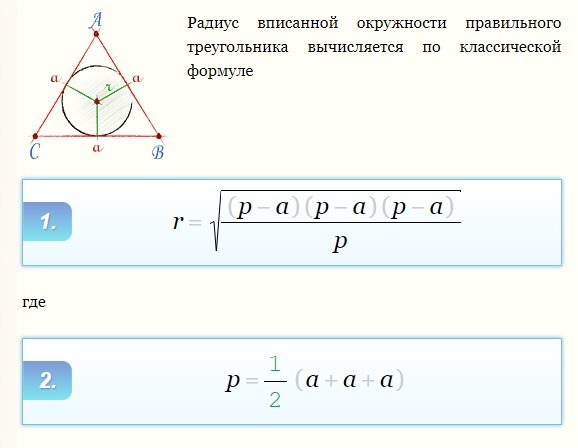
ФОРМУЛЫ для правильного треугольника:

Радиус описанной окружности: R = a/√3 = 8/√3 = 8/3*√3 - ОТВЕТ

Радиус вписанной окружности: r = a/(2*√3) = 4/√3 = 4/3*√3 - ОТВЕТ

Answer 2

я написал радиус описанной и диаметр окружности

Answer 3

Радиус описанной находим через формулу 2R=a/sina, находим Радиус вписанной окружности по формуле S=rp, диаметр равен двум радиусам, значит d=2r.