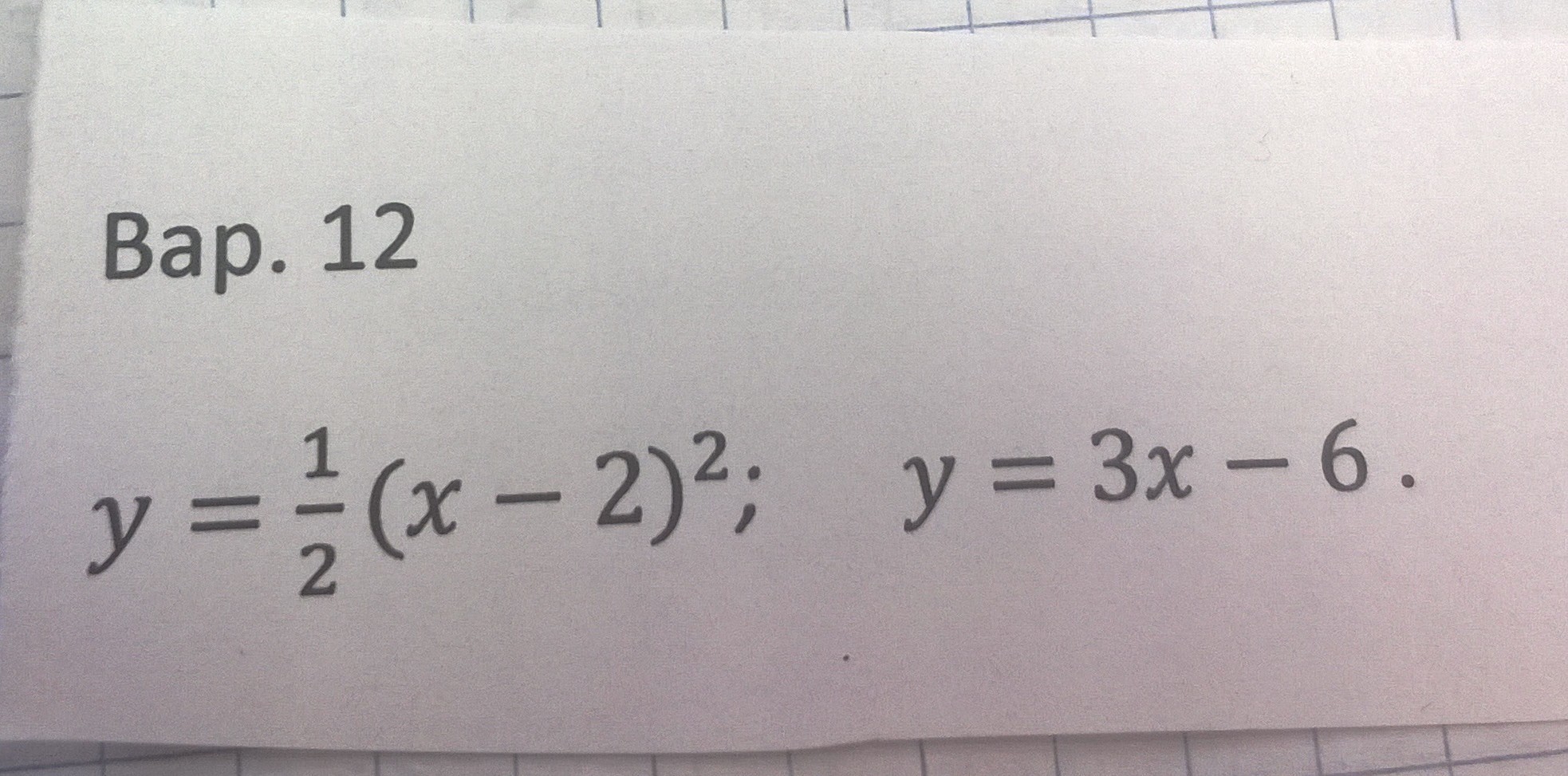Question

y=1/2(x-2)^2 y=3x-6 найти площадь фигуры ограниченной линией

Answer 1

Площадь фигуры, ограниченной линиями интеграл вида:

$intlimits^a_b {(y_1 - y_2)} , dx$, где a,b - точки пересечения графиков.

Найдем точки пересечения:

(x-2)²/2 = 3x-6;

x²-10x+16=0

D=100-4*16=36

x₁=(10+6)/2 = 8

x₂=(10-6)/2 = 2

Тогда площадь:

$S = intlimits^2_8 {x^2-10x+16} , dx$

S = (3(8)³-20(8)²+16(8)) - (3(2)³-20(2)²+16(2)) = 384 - 24 = 360

Answer 2

разве в интеграле сверху не большая граница?