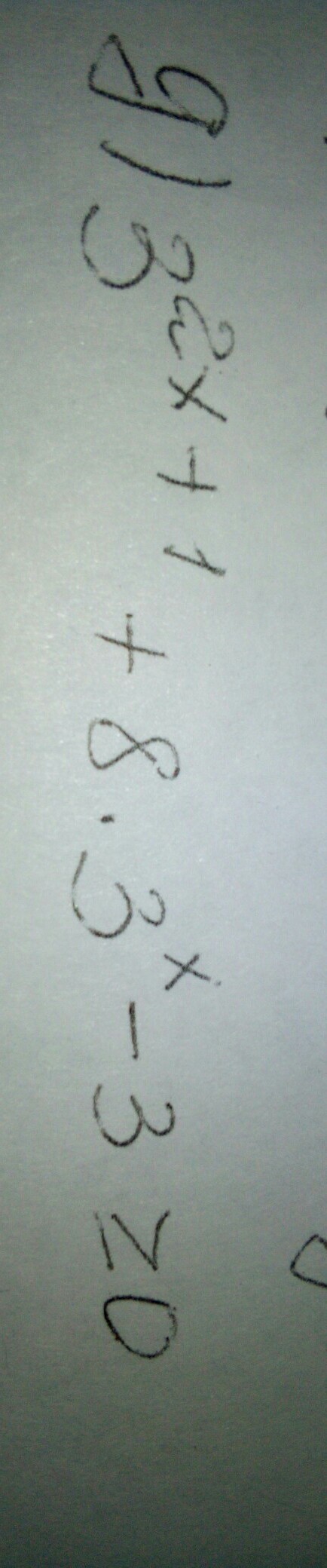Question

допоможіть будь ласка

Answer 1

$3^{2x+1}+8*3^x-3geq 0\\3*3^{2x}+8*3^x-3geq 0\\t=3^x, t>0\3t^2+8t-3geq 0$

$D=64-4*3*(-3)=100\\t_1=1/3\t_2=-3$

$3(t-1/3)(t+3)geq 0\tin (-infty,-3] U [1/3, +infty)$

Т.к. t>0, то второй корень не удовлетворяет условию ОДЗ. Равно как и весь первый полуинтервал полученных значений неравенства.

Значит, остается только второй.  Найдём x: $3^x=t_1=1/3 => x=-1$

Значит, решением неравенства будет: $xin[-1,+infty)$

Answer 2

Распиши первое слагаемое произведением.  3^(2x)*3^1+8*3^x-3≥0

Замена 3^x=t

3t²+8t-3≥0. Корни -3 и 1/3.

3(t+3)(t-1/3)≥0. Решения t≤-3 или t≥1/3/

3^x≤-3  или 3^x≥1/3. Вт  первом неравенстве решений нет а во втором х≥-1.    Ответ :[-1; +∞).