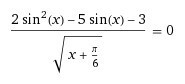Ответы
Ответ дал:
0
ОДЗ: x+π/6>0 ⇒ x>-π/6
С учетом ОДЗ:
Ответ:
Ответ дал:
0
Спасибо <З
Ответ дал:
0
{2sin²x-5sinx-3=0
{x+π/6>0
1)2sin²x-5sinx-3=0
sinx=t
2t²-5t-3=0
t=(5±7)/4
t1=3
t2=-1/2
sinx=3;x€∅
sinx=-1/2
x=(-1)ⁿ(-π/6)+πn
1)n чётний
x1=-π/6+2πk
2)n не чётний
x2=7π/6+2πn
2)x1+π/6>0
-π/6+2πk+π/6>0
2πk>0
k>0
x2+π/6>0
7π/6+2πn+π/6>0
8π/6+2πn>0
8π+12πn>0
n>-8π/12π
n>-2/3
n={0;1;2;3;...........}
[k={1;2;3;........};x1=-π/6+2πk
[n={0;1;2;3;. ...};x2=7π/6+2πn
{x+π/6>0
1)2sin²x-5sinx-3=0
sinx=t
2t²-5t-3=0
t=(5±7)/4
t1=3
t2=-1/2
sinx=3;x€∅
sinx=-1/2
x=(-1)ⁿ(-π/6)+πn
1)n чётний
x1=-π/6+2πk
2)n не чётний
x2=7π/6+2πn
2)x1+π/6>0
-π/6+2πk+π/6>0
2πk>0
k>0
x2+π/6>0
7π/6+2πn+π/6>0
8π/6+2πn>0
8π+12πn>0
n>-8π/12π
n>-2/3
n={0;1;2;3;...........}
[k={1;2;3;........};x1=-π/6+2πk
[n={0;1;2;3;. ...};x2=7π/6+2πn
Ответ дал:
0
Спасибо ~~~
Вас заинтересует
3 года назад
3 года назад
9 лет назад
9 лет назад
10 лет назад