ООООООЧЕНЬ ОЧЕНЬ СРОЧНО ПОЖАЛУЙСТА !!!!!
Свинцовая пуля, которая двигалась со скоростью 300 м/с , Ударилась о металлическую пластину и остановилась. Какая часть свинца расплавилась, если считать, что свинец полностью поглотил энергию, которая выделилась при ударе? Начальная температура шара 27 ∘ С . (Нужен приблизительный ответ)
Ответы
Ответ дал:
0
Дано:
Скорость пули: V = 300 м/с.
Начальная температура свинца: t₁ = 27 °C.
Температура плавления свинца: t₂ = 327 °C.
Удельная теплоёмкость свинца: с = 140 Дж/(кг * °С).
Удельная теплота плавления свинца: λ = 25000 Дж/кг.
Обозначим массу всей пули через m₁, а массу расплавленной части пули через m₂.
Найти отношение масс:
Решение:
0. Кинетическая энергия летящей пули переходит в теплоту нагревания свинца и его плавления, то есть:
1. Кинетическая энергия летящей пули:
2. Энергия (теплота) нагревания пули:
3. Теплота плавления части пули:
4. Объединяем (0), (1), (2) и (3):
5. Выразим искомое отношение из (4).
Численно получим:
Ответ: 0,12 часть.
Ответ дал:
0
Я считаю, что Ваше решение неверное. Кинетич. энергия пули ушла на нагревание ВСЕЙ пули и оставшаяся часть на плавление ее части. См. мое решение ниже.
Ответ дал:
0
Думаю, вы правы.
Ответ дал:
0
Решение на фото. Расплавилась только 1/8 всей пули.
Приложения:
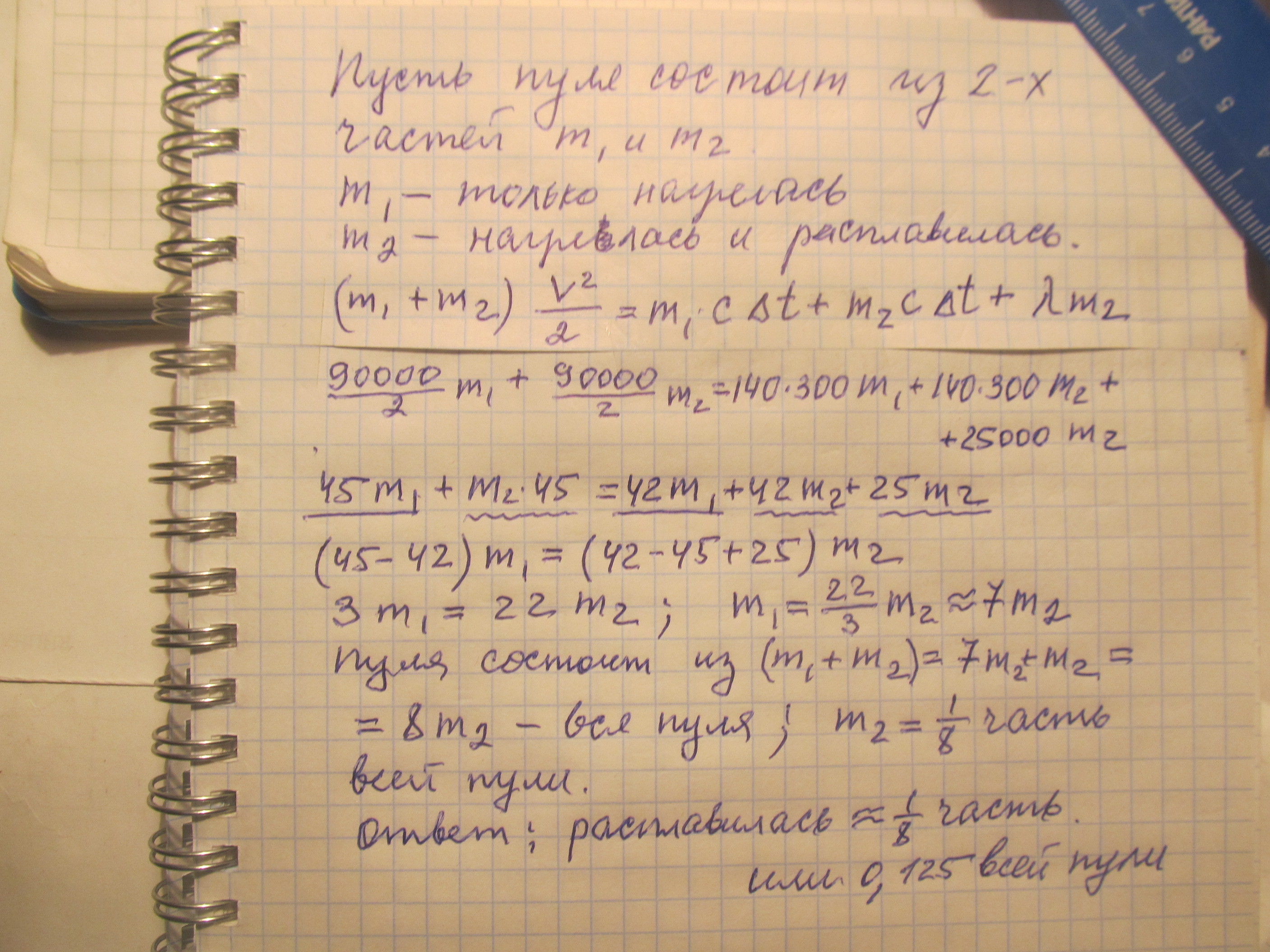
Вас заинтересует
2 года назад
2 года назад
3 года назад
9 лет назад
9 лет назад
10 лет назад
10 лет назад