Question

ДАЮ 30 БАЛЛОВ, СРОЧНО!!!

Прямоугольник вписан в квадрат так, что его стороны параллельны диагоналям квадрата, а вершины лежат на сторонах квадрата. Найдите периметр прямоугольника, если длина диагонали квадрата равна 10,5

Answer 1

∠А=90-60=30°.тогда ВМ=1/2*10=5-как катет против угла 30°.

s=(BC+AD)/2*BM

s=(4+10,5/2*5)=30,25

Answer 2

Ответ: 21 (ед. длины)

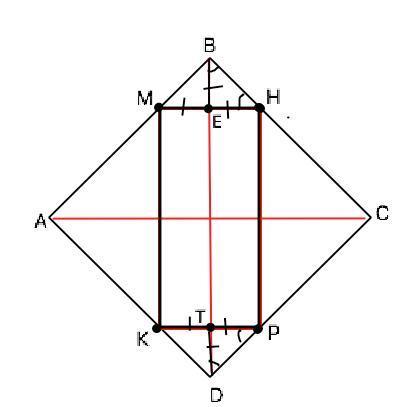
Объяснение: Поскольку стороны вписанного прямоугольника параллельны диагоналям квадрата,  диагональ ВD квадрата   делит периметр прямоугольника на две равные половины ТКМЕ и ТРНЕ. Как известно, диагонали квадрата делят его углы пополам.  При этом угловые треугольники МВН и КDР – равные прямоугольные  равнобедренные, в которых ВЕ=ЕМ=ЕН и TD=ТК=РТ.  Заметим, что МК+МЕ+ТК=DВ=10,5 - это длина половины периметра прямоугольника. Полный периметр прямоугольника КМНР=2•10,5=21 ( ед. длины)