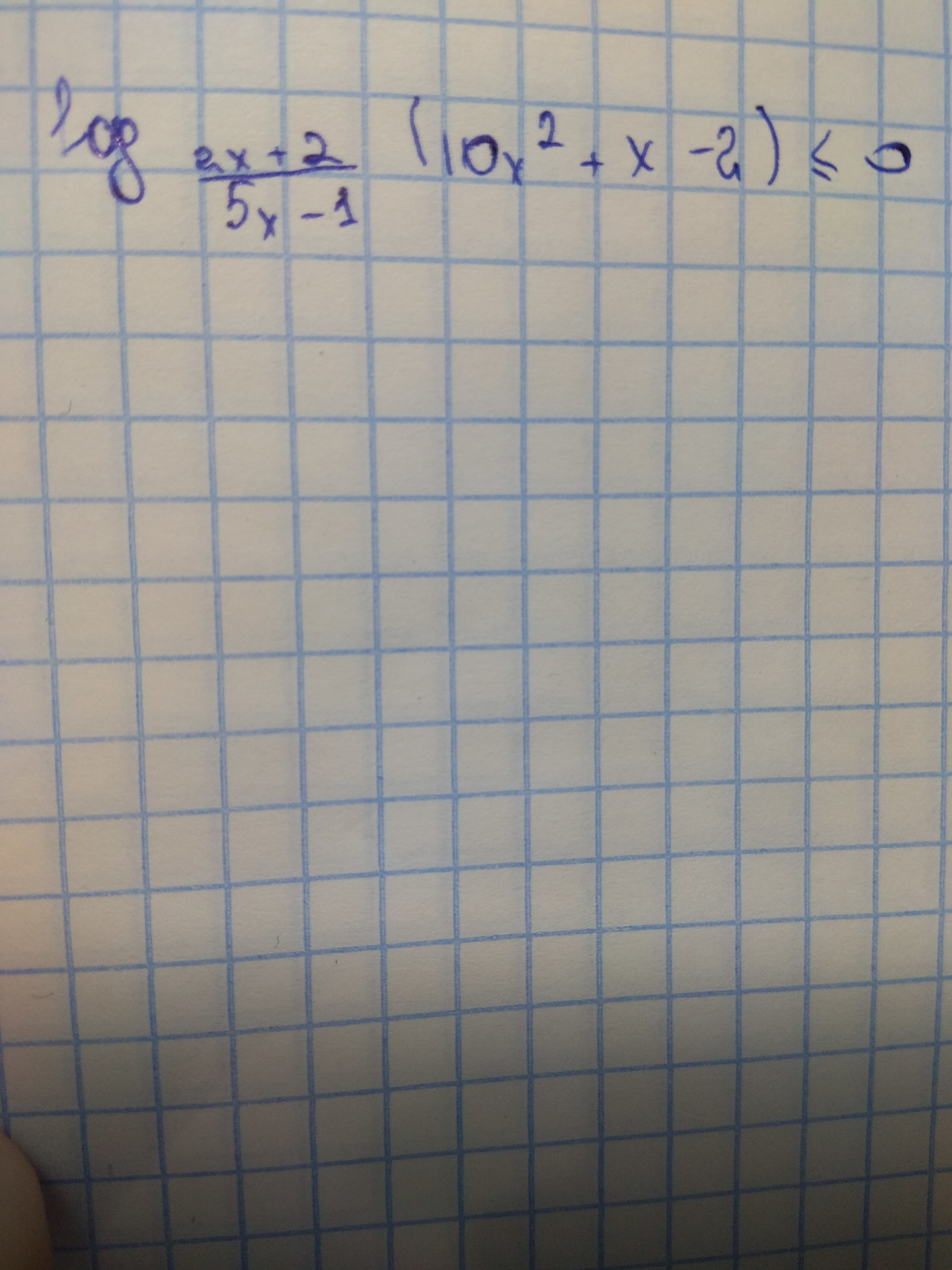Ответы
Ответ дал:
0
ОДЗ:
Воспользуемся следующим методом рационализации:
В частности, так как ,
Тогда исходное неравенство станет равносильным неравенству:
Решим неравенство методом интервалов (см. рис.). Получим, что
Объединяя полученный промежуток с ОДЗ, получим ответ.
Ответ:
Приложения:
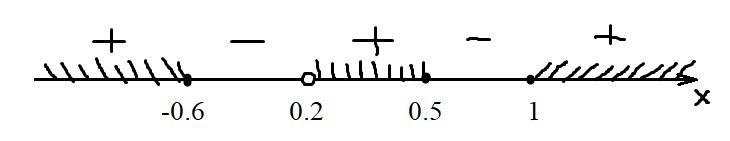
Вас заинтересует
2 года назад
2 года назад
3 года назад
9 лет назад
9 лет назад
10 лет назад