Помогите пожалуйста. Хотя бы 1 букву. Если решите обе, отмечу как лучшее. Даю 40 баллов
Приложения:
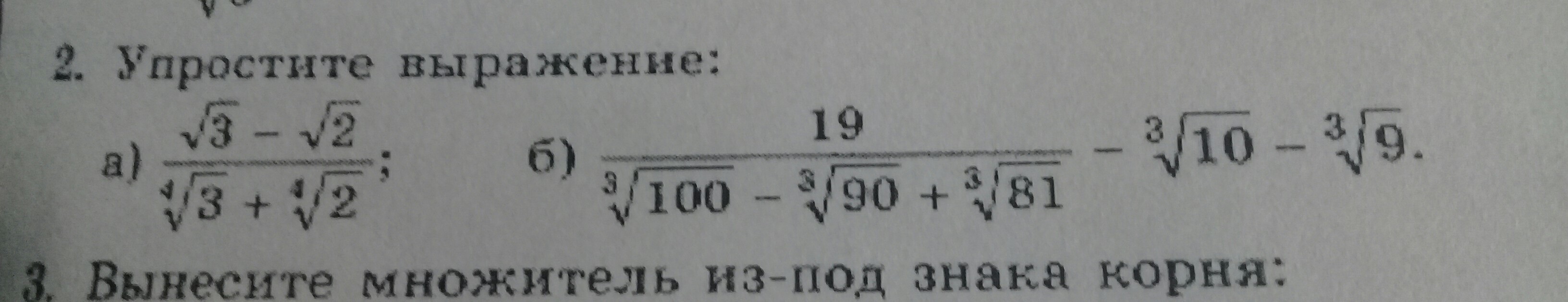
Ответы
Ответ дал:
0
а)
б)
Ответ дал:
0
Жаль, что не сделал подстановку.
Ответ дал:
0
а) Решается заменой переменной. Получается формула "разность квадратов".
Получаем выражение:
б) Формула для разности кубов.
Делаем замену переменных
Ответ дал:
0
Вот такой вопрос под а) Для того что бы избавиться от иррациональности надо И числитель И знаменатель множить на сопряженный знаменатель. А у вас только числитель, я возможно что то не так поняла, но можете объяснить пожалуйста ?
Ответ дал:
0
Никакой иррациональности не стало после подстановки.
Ответ дал:
0
Получаются - разность квадратов в задаче а) и сумма кубов в задаче б)
Ответ дал:
0
Да да, это понятно
Вас заинтересует
3 года назад
3 года назад
9 лет назад
9 лет назад
10 лет назад