Question

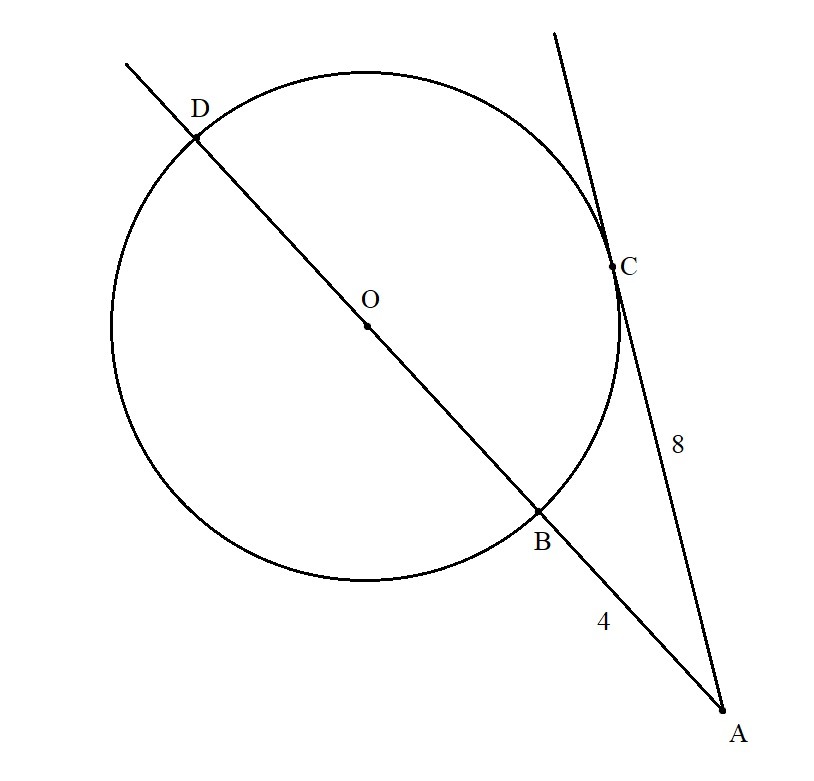
дан круг с центром в точке О. из точки А что не принадлежит этому кругу к ниму провдено касающюю АС и секущую ОА. секущая АО пересекает круг в точках В и D. найти радиус этого круга если АВ=4 см, а АС=8 см

Answer 1

По свойству касательной и секущей $AC^2=AB*AD Rightarrow 8^2=4*AD Rightarrow AD=16$ см. Тогда $BD = AD - AB=16-4=12$ см. BD - диаметр, значит, радиус $R = frac{BD}{2}=frac{12}{2} =6$ см.

Ответ: R = 6 см.