Question

Решить неравенство, и график сделать

4-x^2>0

Answer 1

Решить неравенство.

$4 - x^2 > 0;\x^2 - 4 < 0;\(x - 2)(x + 2) < 0;\x in (-2; 2).$

Построить график.

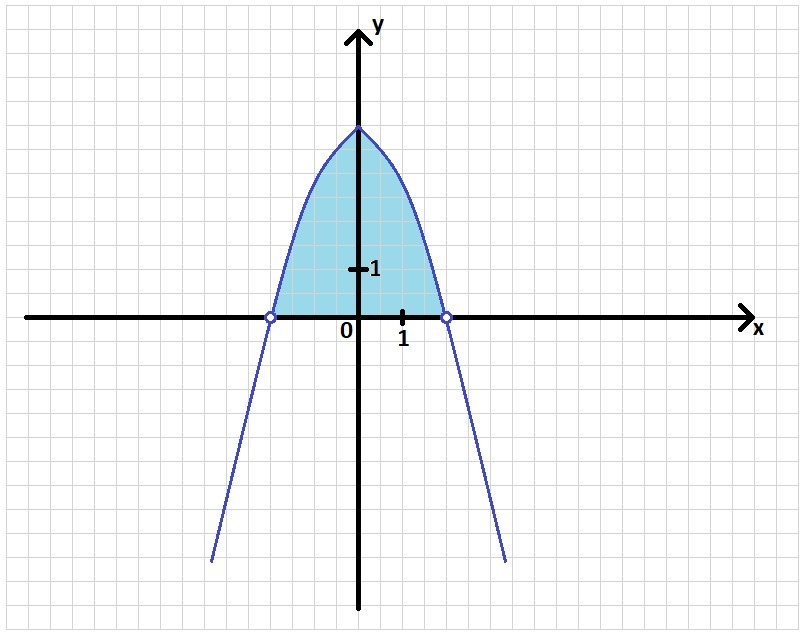
1) Так как имеется квадратный одночлeн, графиком будет парабола.

2) Поскольку перед x² стоит минус, ветви параболы направлены вниз.

3) Найдём координаты вершины.

$x_B = left[dfrac{-b}{2a}right] = dfrac{0}{-2} = 0;\\y_B = 4 - x_0^2 = 4 - 0 = 4.$

Таким образом, вершина находится в точке (0; 4).

4) Найдём точки пересечения параболы с осью абсцисс (Ox).

$[y = 0]: 4 - x^2 = 0;\{}hspace{1,3cm} x^2 = 4;\{}hspace{1,3cm} x = pmsqrt{4};\{}hspace{1,3cm} x = pm2.$

Получаем, что функция пересекает Ox в 2 точках: (-2; 0) и (2; 0).

5) Заштрихуeм требуемый интервал.

Примерный график смотри в приложении.

Answer 2

ты отлично объясняешь, спасибо