Question

#151, помогите, пожалуйста! Даю 15 БАЛЛОВ

Answer 1

Подробное решение в прикрепленном файле.

Answer 2

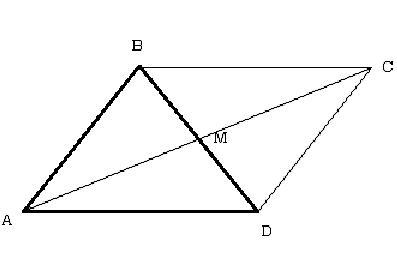
Основание равнобедренного треугольника равна 4√2 см, а медиана, проведенная к боковой стороне, равна 5 см. Найти боковую сторону треугольника.

Решение:

Так как АМ - медиана треугольника ABD, то BM = MD. Достроим до параллелограмма ABCD, в нём BC = AD = 4√2; AB = BD = CD.

AM = CM. Сумма квадратов диагоналей параллелограмма равна сумме квадратов его сторон.

$AC^2+BD^2=2(AB^2+AD^2)\ \ 10^2+BD^2=2cdot (BD^2+(4sqrt{2})^2)\ \ 100+BD^2=2BD^2+64\ \ BD^2=36\ \ BD=8~_{sf CM}$

Ответ: 8 см.