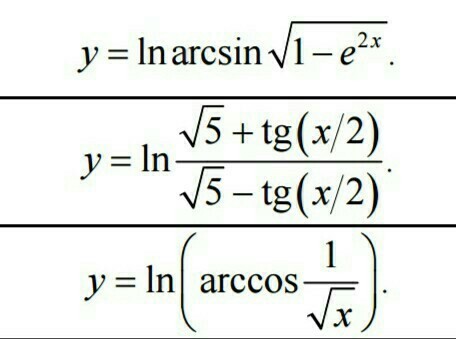Ответы
Ответ дал:
0
Ответ дал:
0
а втором примере не должно быть просто 5, а не √5?
Ответ дал:
0
а во втором*
Ответ дал:
0
В ответе
Ответ дал:
0
В числителе корень из 5, а в знаменателе - просто 5
Ответ дал:
0
y'=(lnarcsin√(1-e^(2x)))'=1/(arcsin√(1-e^(2x))
*(arcsin√(1-e^(2x))'=1/(arcsin√(1-e^(2x)
*1/(√1-(1-e^2x)) *(√(1-e^2x)'=
1/(srcsin√(1-e^2x)*1/e^x *1/(2√1-e^2x) *(-2e^2x)=
1/(arcsin√(1-e^2x) *1/e^x *
(-1/(e^2x*√(1-e^2x))
*(arcsin√(1-e^(2x))'=1/(arcsin√(1-e^(2x)
*1/(√1-(1-e^2x)) *(√(1-e^2x)'=
1/(srcsin√(1-e^2x)*1/e^x *1/(2√1-e^2x) *(-2e^2x)=
1/(arcsin√(1-e^2x) *1/e^x *
(-1/(e^2x*√(1-e^2x))
Вас заинтересует
2 года назад
3 года назад
3 года назад
9 лет назад
9 лет назад