Question

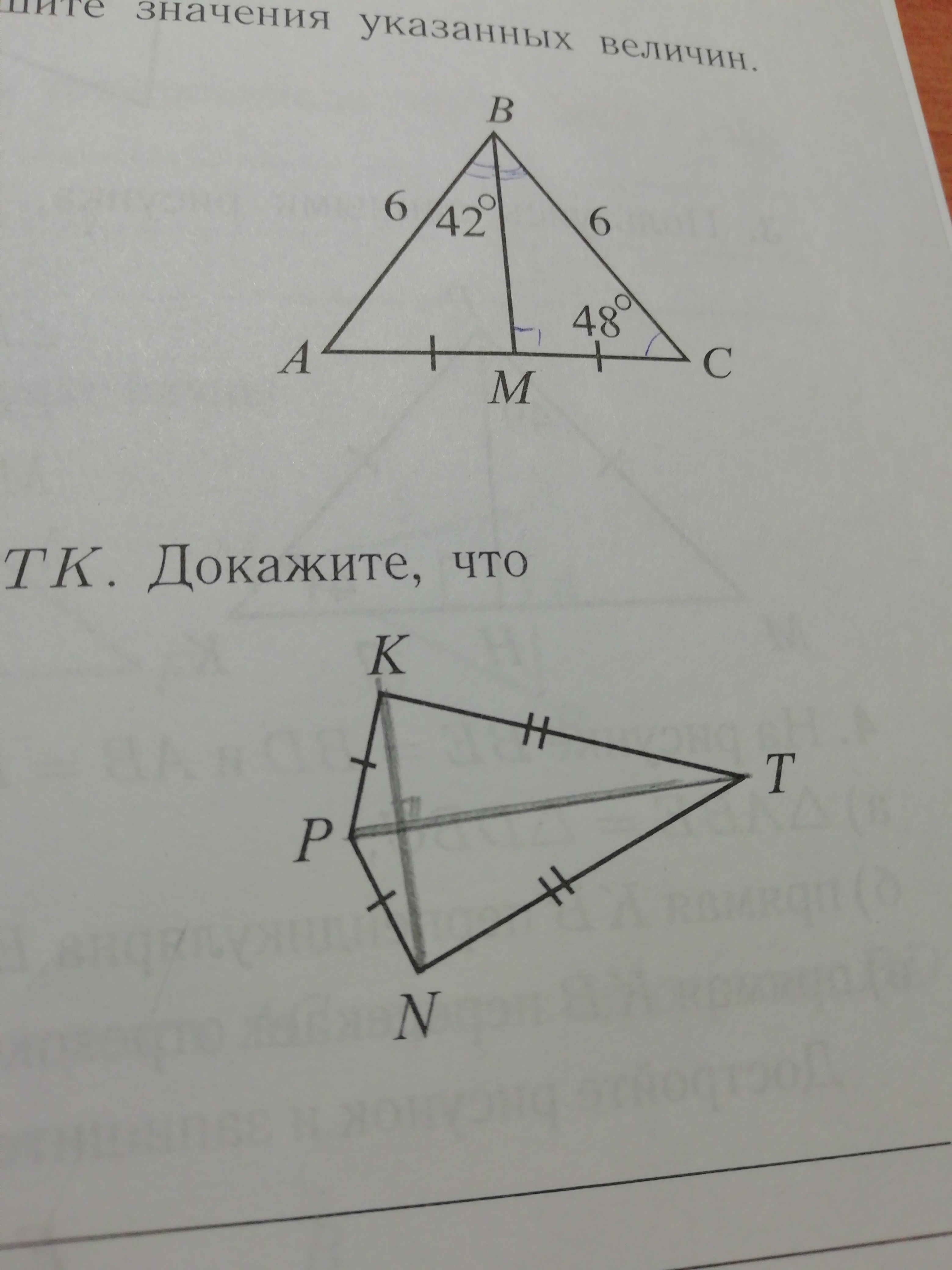
На рисунке NP = PK и NT = TK. Докажите, что

а)треугольник PNT = треугольнику PKT

б)РТ - биссектриса угла Р

в) NK - перпендикулярен РТ

Дано :......

Доказать:.......

Док-во:......

пожалуйста, помогите

Answer 1

Дано:

Выпуклый 4х-угольник PKTN

PN=PK, TK=TN

Доказать:

1) ΔPNT=ΔPKT

2) PT - биссектриса ∠P

3)NK⊥PT

Док-во:

1) Рассмотрим ΔPNT и ΔPKT:

1. PK=PN (по условию)
2. TK=TN (по условию)
3. PT - общая сторона

Из этого всего следует, что ΔΔ= по 3 сторонам.

Ч.Т.Д.

2) Т.к. ΔPNT=ΔPKT, то ∠NPT=∠KPT (если ΔΔ=, то = их соответствующие элементы). Следовательно, PT является биссектрисой ∠P.

Ч.Т.Д.

3) Пусть точка пересечения NK и PT будет названа О.

Т.к. ΔPNT=ΔPKT, то ∠NOP=∠KOP (если ΔΔ=, то = их соответствующие элементы), а т.к. ∠NOP и ∠KOT; ∠KOP и ∠NOT вертикальные, то получается: ∠NOP=∠KOT=∠KOP=∠NOT. Сумма этих углов = 360°, поэтому каждый угол будет=360°:4=90°.

Ч.Т.Д.