Question

решите графически уравнения
sinx+(x+п/2)^2+1=0

Answer 1

Ответ:      - π/2

Пошаговое объяснение:

$sinx+(x+frac{pi}{2})^{2}+1=0\sinx=-(x+frac{pi}{2})^{2}-1$

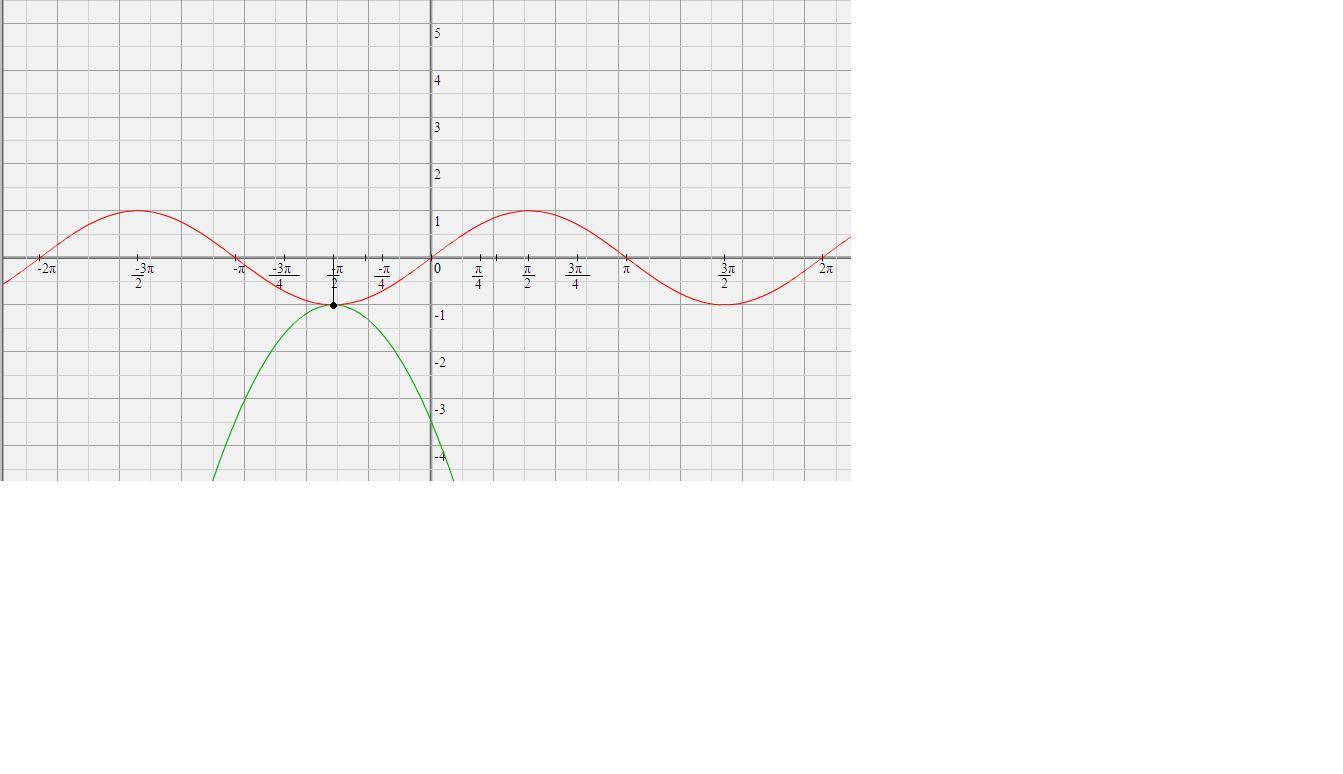
Построим графики функций

f(x) = sin x    и      $g(x)=-(x+frac{pi}{2})^{2}-1$

График функции f(x) - синусоида.

График функции g(x) - парабола, ветви которой направлены вниз, а координаты вершины  ( - π/2 ; - 1).

У графиков единственная точка пересечения ( - π/2 ; - 1).

Значит, корень уравнения х = - π/2.