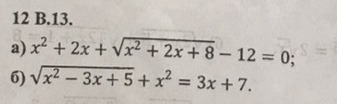Question

помогите пожалуйста решить 50 б

Answer 1

!!!!!!!!!!!!!!!!!!!!!!!!!

Answer 2

a) Обозначим

$sqrt{x^{2}+2x+8 }=m,mgeq 0,$

Тогда x² + 2x + 8 = m² ,  а   x² + 2x = m² - 8

Получим

m² - 8 + m - 12 = 0

m² + m - 20 = 0

D = 1 - 4 * ( - 20) = 1 + 80 = 81 = 9²

$m_{1}= frac{-1+9}{2}=4\\m_{2}=frac{-1-9}{2}=-5$

m = - 5 - не подходит

Значит :

$sqrt{x^{2}+2x+8 }=4\\x^{2} +2x+8=16\\x^{2}+2x-8=0\\D=2^{2}-4*(-8)=4+32=36=6^{2}\\x_{1} =frac{-2+6}{2}=2\\x_{2}=frac{-2-6}{2}=-4$

Ответ : - 4 ; 2

2) Обозначим

$sqrt{x^{2}-3x+5 }=m,mgeq0$

Тогда x² - 3x + 5 = m² ,   а   x² - 3x = m² - 5

Получим

m + m² - 5 - 7 = 0

m² + m - 12 = 0

D = 1² - 4 * (- 12) = 1 + 48  = 49 = 7²

$m_{1}=frac{-1+7}{2}=3\\m_{2}=frac{-1-7}{2}=-4$

m = - 4 - не подходит

Значит

$sqrt{x^{2}-3x+5 }=3\\x^{2}-3x+5=9\\x^{2}-3x-4=0\\D=(-3)^{2}-4*(-4)=9+16=25=5^{2}\\x_{1} =frac{3+5}{2}=4\\x_{2}=frac{3-5}{2}=-1$

Ответ : - 1 ; 4