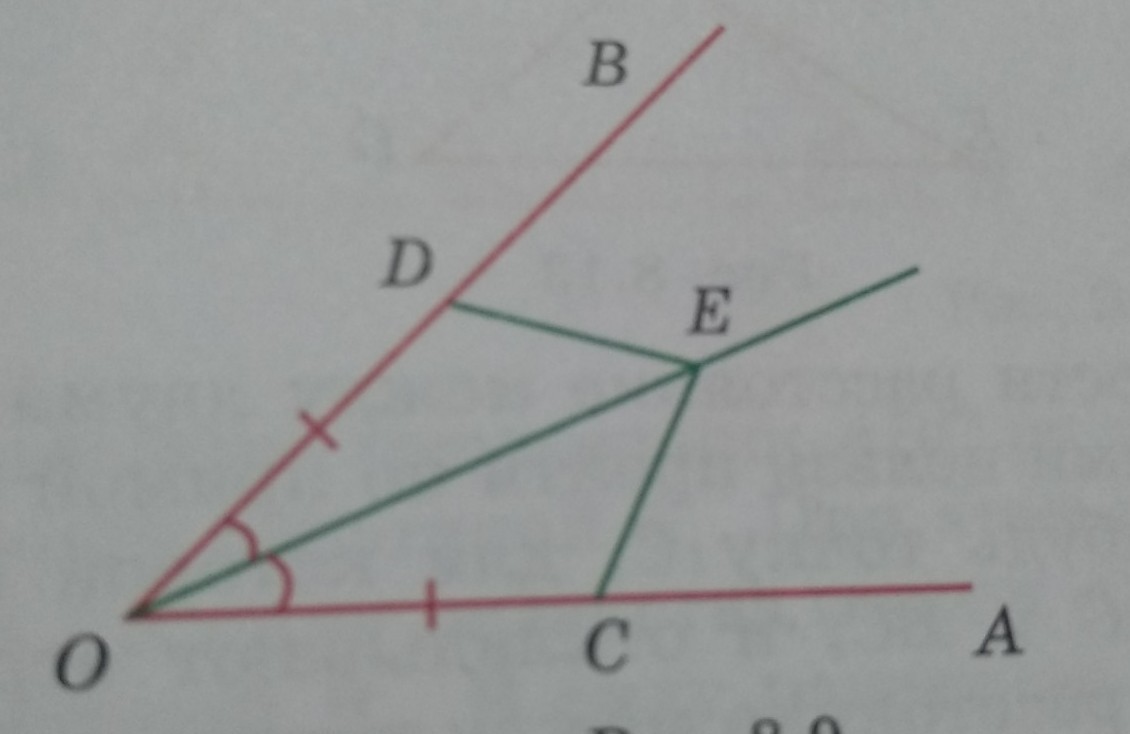
на сторонах угла АОВ отложены равные отрезки ОС и ОD. Произвольная точка Е биссектрисы этого угла соединена с точками C и D. Докажите, что EC = ED.
Приложения:
Ответы
Ответ дал:
0
Рассмотрим треугольник ОДЕ и треугольник ОСЕ. ОД=ОС по условию, <ДОЕ=<СОЕ (ОЕ - биссектриса), ОЕ - общая. Треугольник ОДЕ = треугольнику ОСЕ по двум сторонам и углу между ними (1 признак равенства треугольников). А если треугольники равны, то равны и их стороны. Значит, СЕ=ЕД.
Ответ дал:
0
Докозательство: Рассмотрим углы OBE И EOA. У них равны OC и OD по условию. E - делит углы пополам. Следовательно, применяя первый признай равенства треугольников, EC = ED по двум сторонам и углу между ними .
Вас заинтересует
2 года назад
3 года назад
3 года назад
9 лет назад
9 лет назад
10 лет назад