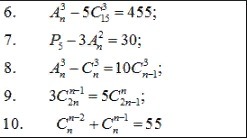Question

Комбинаторика.

Решить уравнение: под цифрой 9

Answer 1

Ответ: n=5

Пошаговое объяснение:

$frac{3(2n)!}{(n-1)!(2n-n+1)!}=frac{5(2n-1)!}{n!(2n-1-n)!}\frac{3(2n)!}{(n-1)!(n+1)!}=frac{5(2n-1)!}{n!(n-1)!}$

Перенесём дроби в одну часть (левую) и вынесем общий множитель.

$frac{(2n-1)!}{n!(n-1)!}left(frac{3(2n)}{n+1}-5right)=0$

Т.к. факториал принимает значения от 1 до плюс бесконечности, то равенство может обратиться в ноль только благодаря разности в скобке.

$frac{6n}{n+1}-5=0\\frac{6n-5n-5}{n+1}=0\\n-5=0 => n=5$

Сделаем проверку:

$frac{3(10)!}{4!6!}=frac{3*7*8*9*10}{2*3*4}=7*9*10=630\\frac{5*9!}{4!5!}=frac{5*6*7*8*9}{2*3*4}=3*5*6*7=630$