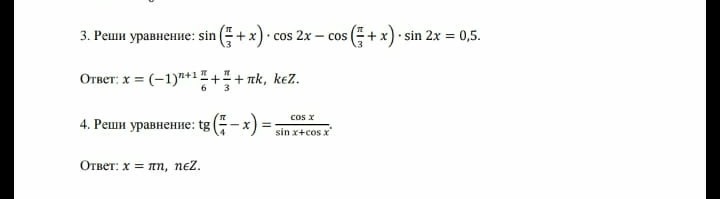Question

Помогите с алгеброй!!!
Ответы даны, нужно само решение.

Answer 1

Решение в скане.....

Answer 2

Спасибооооо!

Answer 3

task/30681465

Решить  уравнение:  3. sin(π/3 +x)*cos2x - cos(π/3 +x)*sin2x  = 0,5

решение   * sin(α - β) = sinα*cosβ - cosα*sinβ,  [ α= π/3+x , β=2x ] *

sin(π/3 +x)*cos2x - cos(π/3 +x)*sin2x =0,5 ⇔ sin(π/3 +x - 2x) = 0,5 ;

sin( -(x -π/3) ) = 0,5 ⇔ - sin(x -π/3) = 0,5 ⇔  sin(x -π/3) = - 0,5 ⇔

x-π/3 = (-1)ⁿ⁺¹π/6 +πn , n  ∈ℤ ⇔ x  = (-1)ⁿ⁺¹π/6 +π/3πn , n  ∈ℤ .

ответ :  x  = (-1)ⁿ⁺¹π/6 +π/3πn , n  ∈ ℤ .

4.  Решить  уравнение: tg(π/4 - x) =cosx / ( sinx+cosx )

решение * *  tg(α - β) = (tgα - tgβ) /(1+ tgα*tgβ) , [ α= π/4 , β = x]  * *

tg(π/4 -x) =cosx / ( sinx+cosx )  ⇔

( tg(π/4)- tgx ) / ( 1+ tg(π/4)*tgx) =cosx / ( sinx+cosx )  , [ tg(π/4) = 1 ] ⇔

(1- tgx ) / ( 1+ tgx)  = cosx / ( sinx+cosx)        [ tgx = sinx /cosx ] ⇔

(cosx- sinx ) / ( cosx +sinx )  = cosx / ( sinx+cosx)    ⇔

(cosx- sinx - cosx ) / ( cosx +sinx )  = 0 ⇔ - sinx / ( cosx +sinx ) =0 ⇔

sinx = 0          * * * очевидно  sinx + cosx =  0 ± 1   = ± 1  ≠ 0 * * *

x = πn , n ∈ ℤ                                  ответ :   x = πn , n ∈ ℤ  

Answer 4

Спасибо))