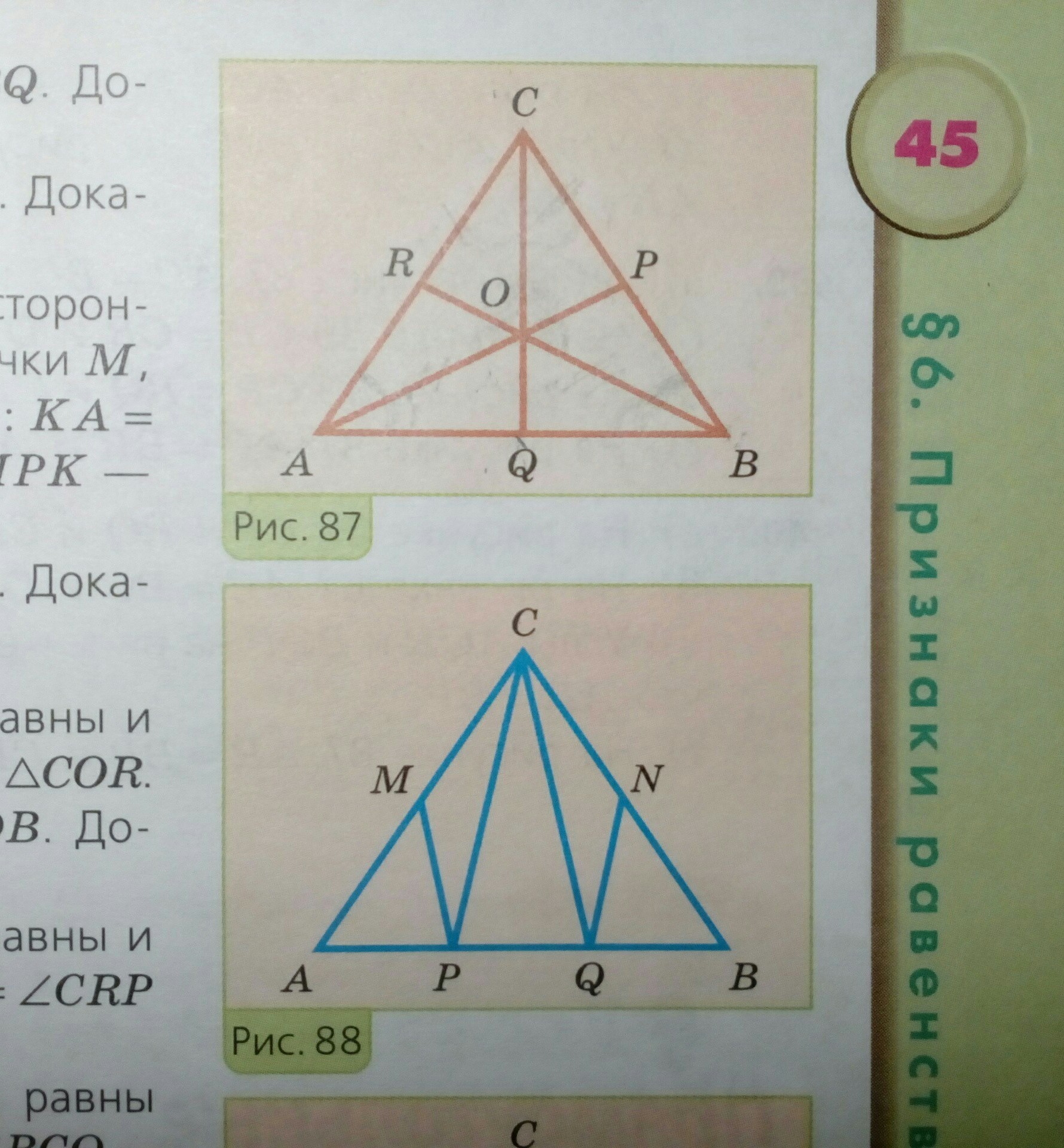
б) На рисунке 87 луч CQ - биссектриса угла ACB, а луч OQ - биссектриса угла AOB. Докажите, что AC=BC
в) Углы ACQ и BCP на рисунке 88 равны и AC=BC. Докажите, что CP=CQ.
С пояснениями, если на листике, пишите аккуратно)) Заранее спасибо:)
(Доказывайте через признак равенства треугольников)
Приложения:
Ответы
Ответ дал:
0
Окей, Допустим.
б) дано: CQ биссектриса ACB
OQ биссектриса AOB
доказать : AC=BC
док-во: рассмотрим треугольники ACQ и BCQ,
CQ общая, а т.к. это биссектриса то AQ=BQ, и углы A=B, следовательно они равны. А если они равны, значит AC=BQ ( по первому признаку)
в) дано: ACQ=BCP AC=BC
доказать: CP=CQ
док-во: ACB- равнобедренный, следовательно, углы САВ и СВА равны. отсюда следует что треугольники ВСР и АСQ равны ( по второму признаку), следовательно CQ=CP
ну, я пыталась.
Вас заинтересует
2 года назад
2 года назад
3 года назад
9 лет назад
9 лет назад