Составьте уравнение касательной и нормали к кривой в точке, соответствующей значению параметра t=t0
Приложения:
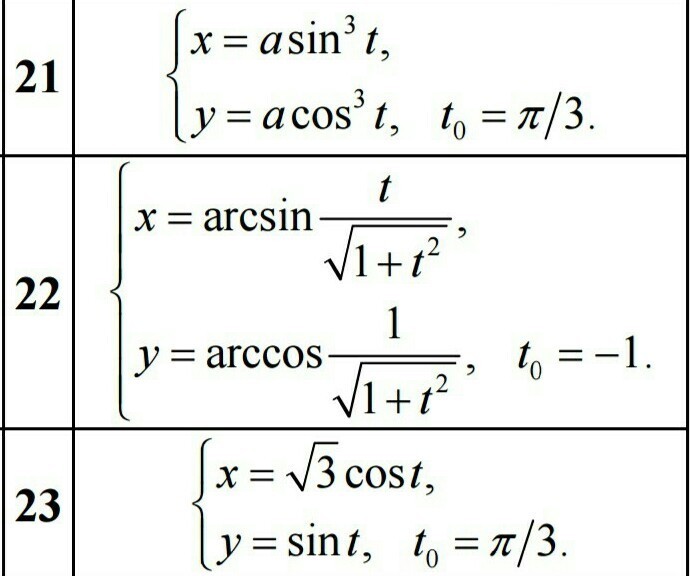
Ответы
Ответ дал:
0
Ответ дал:
0
Добрый вечер! Помогите пожалуйста https://znanija.com/task/30711402
Ответ дал:
0
https://znanija.com/task/30717295?
Вас заинтересует
2 года назад
2 года назад
3 года назад
3 года назад
9 лет назад
9 лет назад
10 лет назад
10 лет назад