Ответы
Ответ дал:
0
(s+p)x²+2sx+s-p=0
(s+p)x²+2sx+(s-p)=0
a=s+p
b=2s
c=s-p
D=b²-4ac
D= (2s)² - 4·(s+p)·(s-p) = 4s² - 4·(s²-p²) = 4s² - 4s² + 4p² = 4p² = (2p)²
Ответ:
Ответ дал:
0
Решаем как обычное квадратное уравнение, где а=s+p, b=2s, c=s-p.
Приложения:
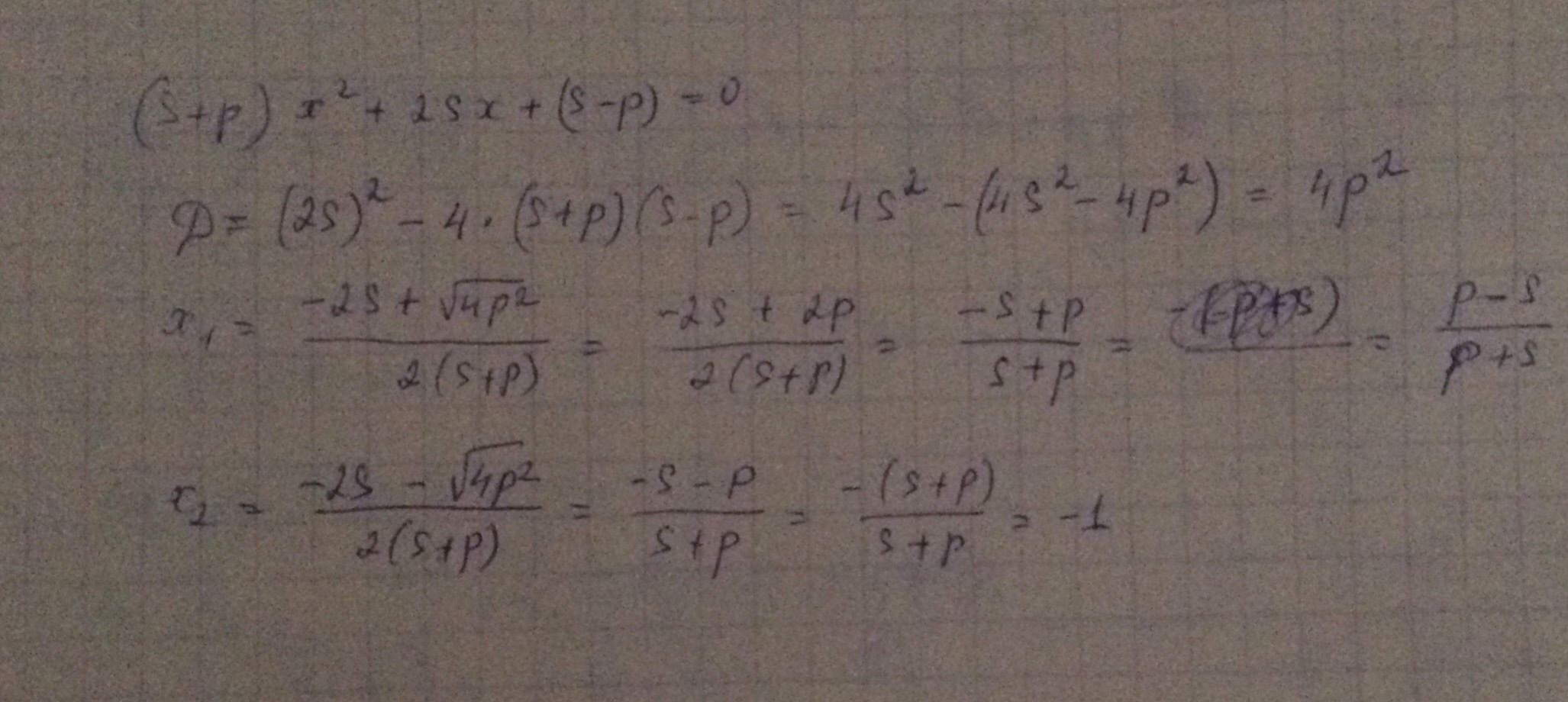
Вас заинтересует
2 года назад
2 года назад
3 года назад
3 года назад
9 лет назад
10 лет назад