Дан куб ABCDA1B1C1D1 с основанием ABCD и боковыми ребрами АА1 , BB1 , CC1 , DD1 , точка M - cередина ребра B1C1. Докажите , что прямые AM и A1C не пересекаются.
Ответы
Ответ дал:
0
ДАНО:
куб ABCDA1B1C1D1
основание ABCD
боковые ребра АА1 , BB1 , CC1 , DD1
M - cередина ребра B1C1
ДОКАЗАТЬ:
AM и A1C не пересекаются
ДОКАЗАТЕЛЬСТВО:
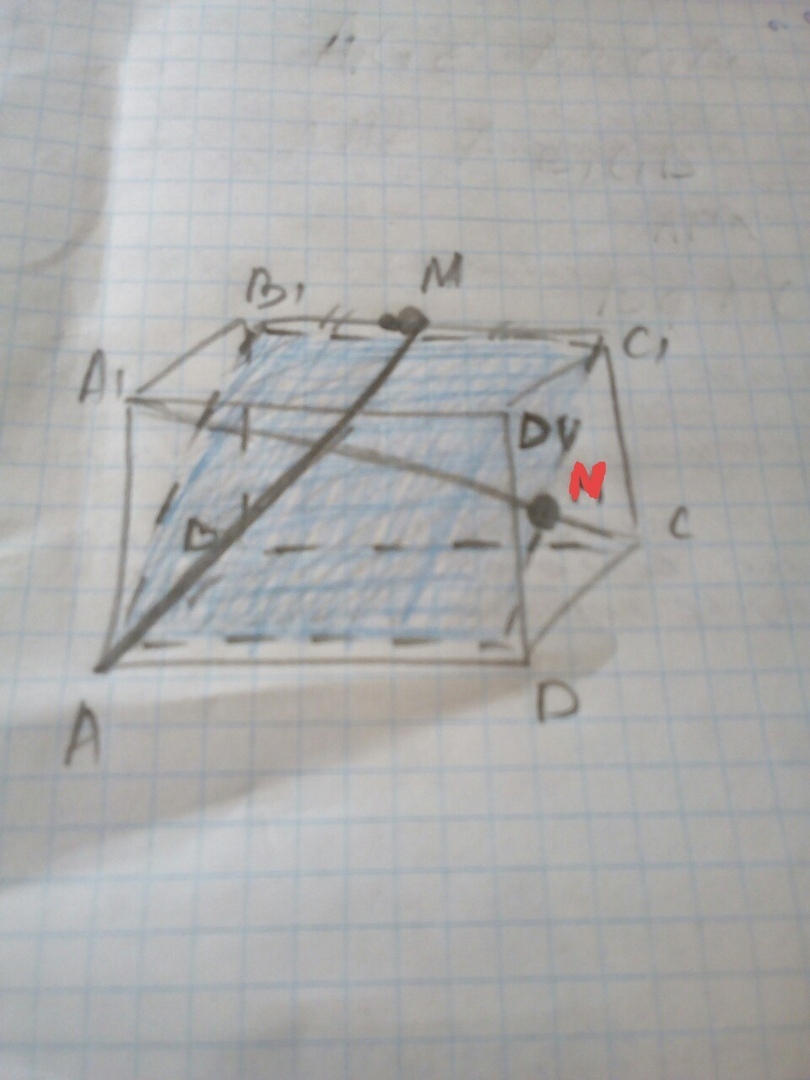
если прямые не пересекаются, они либо параллельны либо скрещиваются. Если бы они были ПАРАЛЛЕЛЬНЫ, то лежали бы в одной плоскости. Но у нас они лежат в разных плоскостях : А1С лежит в плоскости DA1B1C и АМ лежит в плоскости AB1C1D. И А1С пересекает плоскость AB1C1D в точке N. И точка N не принадлежит АМ. Поэтому прямые скрещиваются.
Ответ верный,проверяли))
Приложения:
Вас заинтересует
2 года назад
3 года назад
3 года назад
9 лет назад
10 лет назад