Question

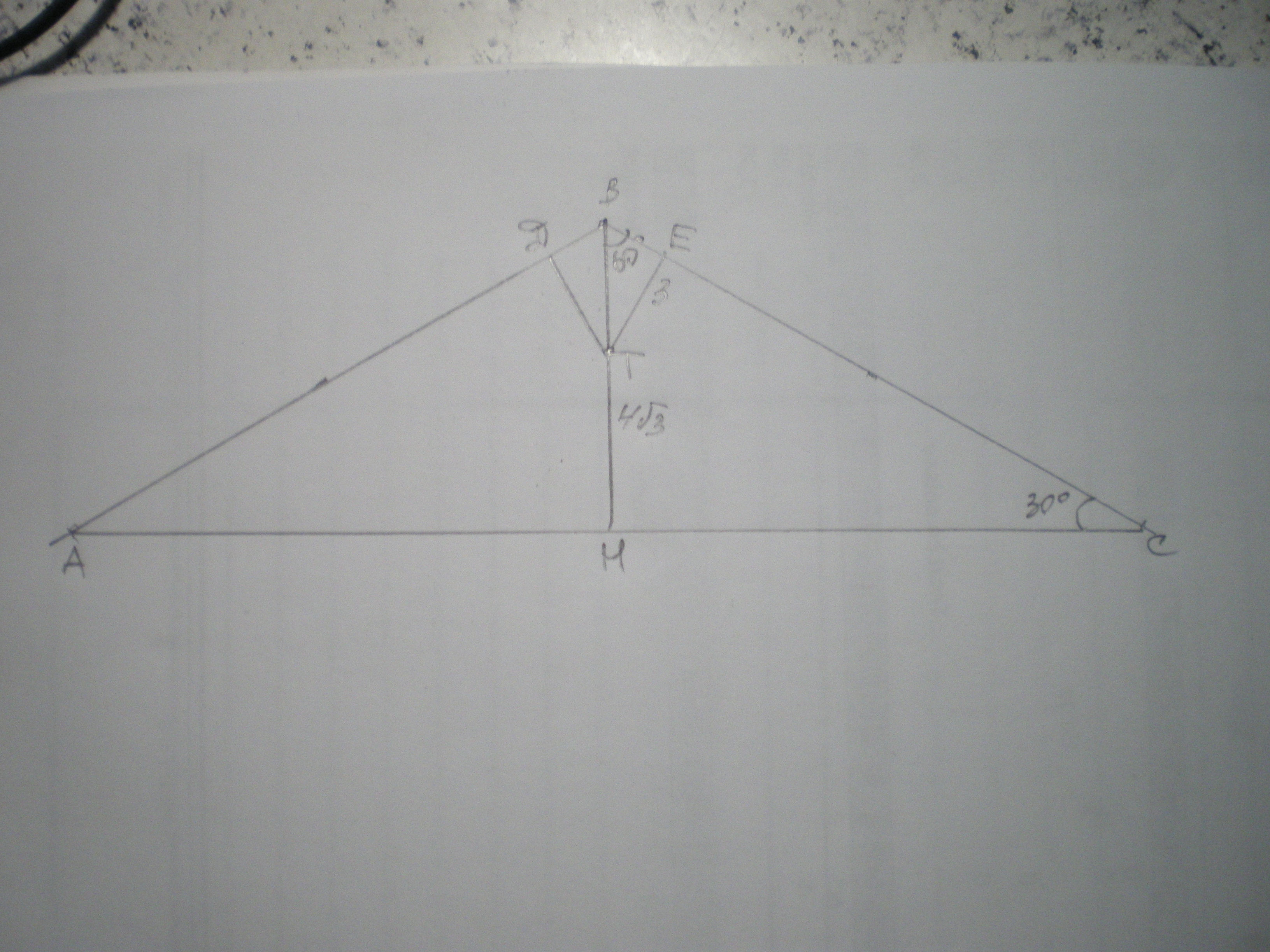
Точка M лежит внутри равнобедренного треугольника с углом при вершине 120º. Расстояние от M до каждой из боковых сторон равно 3, а до основания 4 корня из 3.Найдите длину основания.

Answer 1

Дано: ΔАВС - равнобедренный, АВ=ВС, ∠В=120°, ДТ=ТЕ=3, ТН=4√3. Найти АС.

∠А=∠С=(180-120):2=30°

Поскольку перпендикуляр - кратчайшее расстояние от точки до прямой, ТЕ⊥ВС, а ΔТВЕ - прямоугольный, где ∠ВЕТ=90°.

Таким же образом точка Т находится на перпендикуляре ВН.

Получаем ВН - высота, медиана и биссектриса ∠В,               ∠В=120:2=60°.

Из ΔВТЕ найдем ВТ по теореме синусов:

3sin60=BTsin90; BT=3:√32=2√3.

ВН=ВТ+ТН=2√3+4√3=6√3.

По теореме синусов найдем СН:

6√3sin30=CHsin60

CH=6√3 * √32 : 12 = 18.

АС=2СН=36 (ед.)

Ответ:36 ед.