Question

NNNLLL54 помоги пожалуйста! 20 баллов!
В прямоугольном треугольнике ABC(C=90), высота CH=7, биссектриса = 35/4. Найти катеты и площадь ABC.

Answer 1

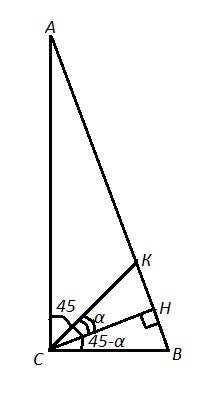
ΔАВС , ∠С=90° , СК- биссектриса  ⇒ ∠АСК=∠ВСК=45° , СН⊥АВ  ⇒  ∠СНВ=90°, СН=7 ,  СК=35/4 .

Рассм. ΔСКН - прямоугольный. Обозначим ∠КСН=α  ,

КН=√(СК²-СН²)=√((35/4)²-7²)=√(441/16)=21/4 .

tgα=КН/СН=21/4:7=3/4 .

Рассм. ΔВСН. ∠ВСН=∠ВСК-∠КСН=45°-α  ⇒  ∠В=90°-(45°-α)=45°+α .

tg∠ВСН=tg(45°-α)=ВН/СН  ⇒  ВН=СН·tg(45°-α)=7·tg(45°-α) .

$tg(45^circ -alpha )=frac{tg45^circ -tgalpha }{1+tg45^circ cdot tgalpha }=frac{1-3/4}{1+3/4}=frac{4-3}{4+3}=frac{1}{7}$

$BH=7cdot frac{1}{7}=1$

$BC=sqrt{BH^2+CH^2}=sqrt{1^2+7^2}=sqrt{50}=5sqrt2$

Рассм. ΔАСН. ∠АСН=∠АСК+∠КСН=45°+α .

tg∠АСН=АН/СН  ⇒  АН=СН·tg∠АСН=7·tg(45°+α)

$tg(45^circ +alpha )=frac{tg45^circ +tgalpha }{1-tg45^circ tgalpha }=frac{1+3/4}{1-3/4}=frac{4+3}{4-3}=7\\AH=7cdot 7=49\\AC=sqrt{AH^2+CH^2}=sqrt{7^2cdot tg^2(45^circ +alpha )+7^2}=7sqrt{49+1}=\=7cdot sqrt{50}=35sqrt2\\AB=AH+HB=49+1=50\\S(ABC)=frac{1}{2}cdot ABcdot CH=frac{1}{2}cdot 50cdot 7=175$

Или:  $S(ABC)=frac{1}{2}cdot ACcdot BC=frac{1}{2}cdot 35sqrt2cdot 5sqrt2=35cdot 5=175$  .