Question

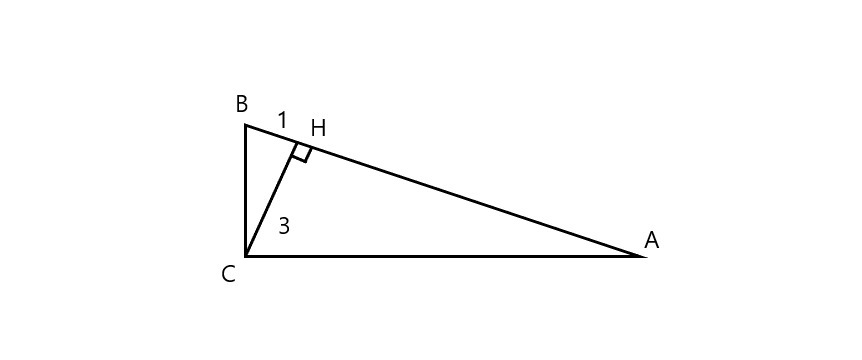
СРОЧНО!!! В прямоугольном треугольнике ABC с прямым углом при вершине C высота CH=3, BH=1. Найдите площадь треугольника ABC.

Answer 1

CH² = AH · HB ⇒

9 = AH · 1 ⇒

AH = 9, откуда площадь:

S = ((AH + HB) · CH) / 2 = 30 / 2 = 15 ед²

Answer 2

Это написал человек, у которого некогда не было ошибок

Answer 3

Не волнуйся)))

Answer 4

Извиняюсь, S = (AH * CH) / 2

Answer 5

Так что там 13.5

Answer 6

и это не верно))) вот и антиспамер тут

Answer 7

Квадрат высоты проведенный из вершины прямого угла треугольника равен произведению длин отрезков отсекаемых этой высотой.

СН²=ВН*АН, 9=1*АН, АН=9, тогда АВ=АН+ВН=10;

Площадь треугольника - половина основания умноженная на высоту проведенную к ней: 10*3/2=15 ед².