Question

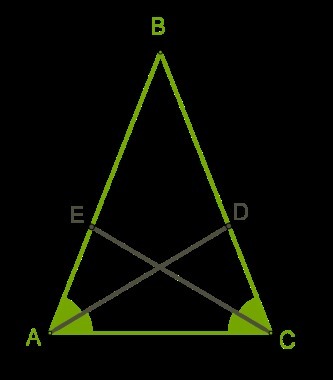
В равнобедренном треугольнике проведены биссектрисы углов, прилежащих к основанию. Определи длину биссектрисы угла ∡A, если длина биссектрисы угла ∡C равна 11 см.
Рассмотрим треугольникиΔDAC и Δ???
(все углы и стороны нужно записывать большими латинскими буквами)

1. Углы, прилежащие к основанию равнобедренного треугольника,
. Так как данный треугольник равнобедренный, то∡B??=∡BCA.
2. Так как проведены биссектрисы этих углов, справедливо, что ∡ =∡DAC=∡DCE= ∡.???
3. У рассматриваемых треугольников общая сторона ???
Значит треугольники равны по второму признаку равенства треугольников.
У равных треугольников равны все соответствующие элементы, в том числе стороны
? = ?
Длина искомой биссектрисы
?см.

Длина искомой биссектрисы
?см.

Answer 1

Решение: рассмотрим треугольник АВDи треугольник СЕВ:
1АВ=ВС по определению равнобедренного треугольника
2 угол В общий
3угол ВАС= углу ВСА по свойству равнобедренного треугольника, а угол ВСЕ=углу ВАD как половины равных углов
Значит, треугольник АВD= треугольнику СЕВ по стороне и двум прилежащим к ней углам ( второй признак). АD=СЕ=11см по свойству равных треугольников.
Ответ: АD=11см.