Question

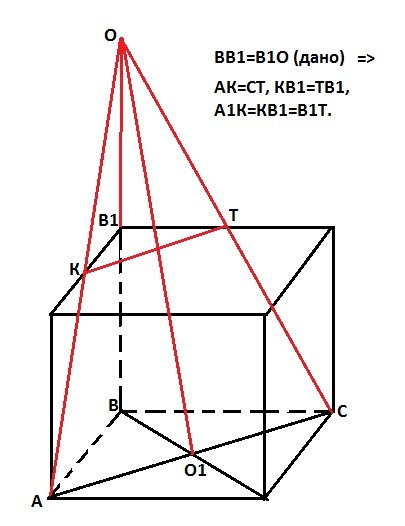
ABCDA1B1C1D1 — куб. Четырехугольник AKTC— сечение куба плоскостью, проходящей через вершины А, С и точку О такую, что точка B1 — середина отрезка ОВ. Докажите, что четырехугольник АKТС — равнобедренная трапеция, и вычислите длину ее средней линии, если длина ребра куба равна 2 см.

Answer 1

1. АВСD - квадрат. Диагонали квадрата взаимно перпендикулярны и точкой пересечения О1 делятся пополам. Следовательно, прямая ОО1 - перпендикулярна АС по теореме о трех перпендикулярах, так как ВО (перпендикулярная АС) - проекция наклонной ОО1. Тогда треугольник АОС - равнобедренный (ОО1 - высота, медиана и биссектриса), АО=ОС и КТ - его средняя линия (так как ВВ1=В1О - дано)  =>  АК=ТС  =>  четырехугольник АКТС - равнобедренная трапеция. Что и требовалось доказать.

2. Средняя линия трапеции - полусумма ее оснований. АС=2√2см (диагональ квадрата со стороной = 2см), а КТ=√2 (по Пифагору, так как треугольник КВ1Т - прямоугольный, равнобедренный, с катетами = 1). Тогда средняя линия трапеции равна 1,5*√2 см.

Answer 2

спасбо

Answer 3

помоте пожалуйста https://znanija.com/task/30886924

Answer 4

почему при вычислении средней линии трапеции ты умножаешь, хотя пишешь чтобы её найти нужно сложить. "Средняя линия трапеции - ПОЛУСУММА ее оснований". И откуда взялось число 1,5 ???